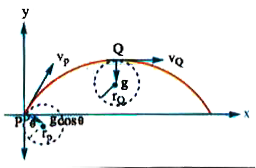
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is projected with a velocity bar(v) = ahat(i) + bhat(j) ....
Text Solution
|
- A particle is projected at angle theta with horizontal with velocity v...
Text Solution
|
- A particle is projected with speed u at angle theta to the horizontal....
Text Solution
|
- A particle is projected with a velocity vecv=ahati+bhatj. Find the rad...
Text Solution
|
- A particle is projected from ground at an angle theta with horizontal ...
Text Solution
|
- A particle is projected with a velocity bar(v) = ahat(i) + bhat(j) ....
Text Solution
|
- A particle is projected from the ground with an initial speed of u at ...
Text Solution
|
- A particle is projected fro the ground with an initial speed v at an a...
Text Solution
|
- A particle is projected from the ground with an initial speed v at an ...
Text Solution
|