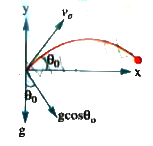Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
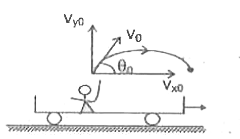
- A boy is standing inside a train moving with a constant velocity of ma...
Text Solution
|
- A ball moving vertically downward with a speed of 10 m//s collides wit...
Text Solution
|
- A boy throws up a ball vertically insided an elevator, with a velocity...
Text Solution
|
- A ball is projected vertically up wards with a velocity of 100 m/s. Fi...
Text Solution
|
- A person sitting in a train moving at constant velocity throws a ball ...
Text Solution
|
- एक ट्रैन समान त्वरण a से एक सीधी रेखा पर चल रही है। ट्रैन में खड़ा एक ल...
Text Solution
|
- A boy is standing inside a train moving with a constant velocity of ma...
Text Solution
|
- A person sitting in a train moving at constant velocity throws a ball ...
Text Solution
|
- A boy is standing inside a train moving with a constant velcoity of ma...
Text Solution
|