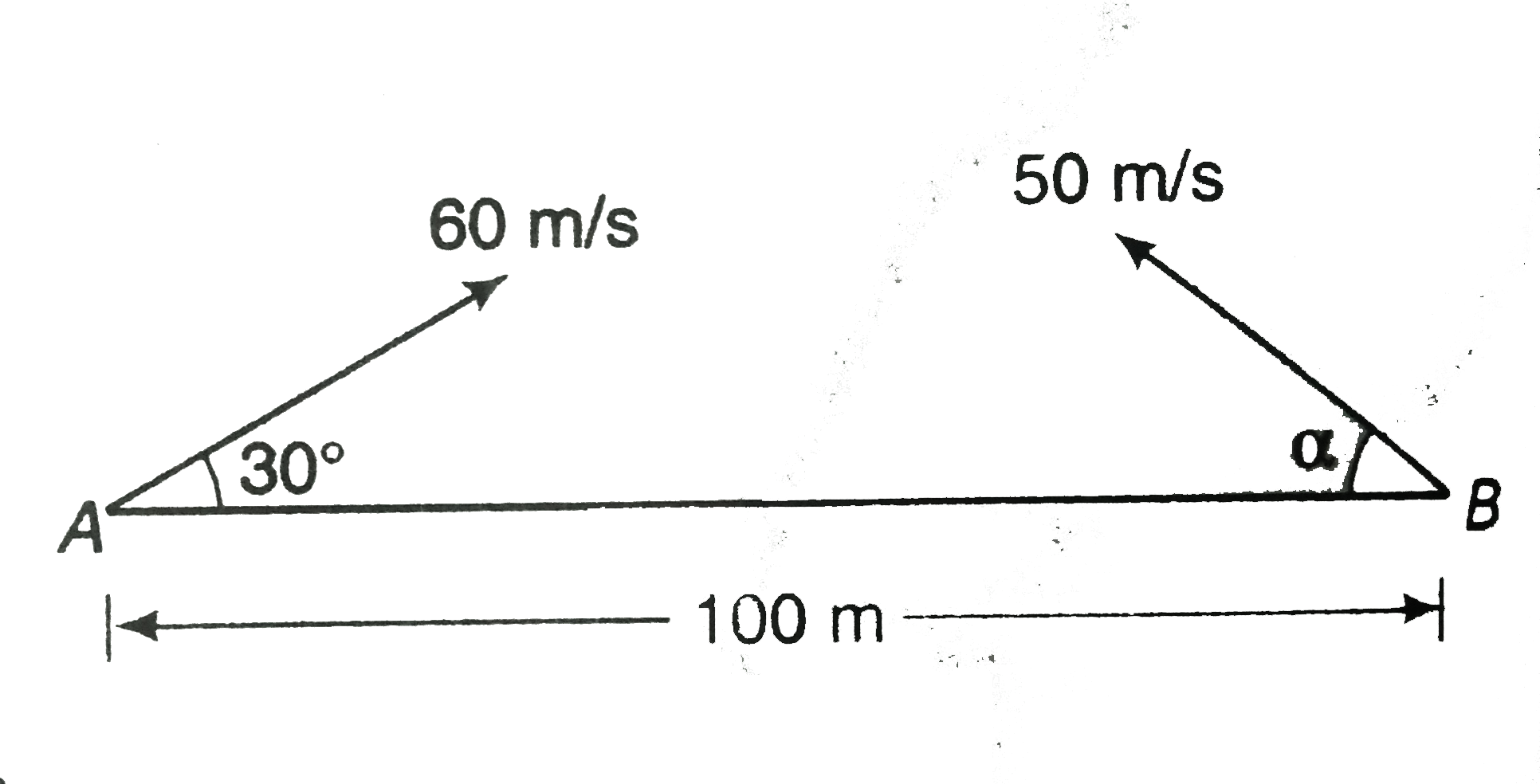Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle A is projected with an initial velocity of 60 m//s at an an...
Text Solution
|
- A particle A is projected with an initial velocity of 60 m//s at an an...
Text Solution
|
- A particle is projected with an initial velocity of 200 m//s in a dir...
Text Solution
|
- A particle A is projected from the ground with an initial velocity of ...
Text Solution
|
- Two particle are projected with same initial velocities at an angle 30...
Text Solution
|
- A particle A is projected with an initial velocity of 60m/s at angle 3...
Text Solution
|
- Two particles are projected horizontally with same speed 30 m//s but i...
Text Solution
|
- A particle is projected with a velocity 10 m//s at an angle 37^(@) to ...
Text Solution
|
- A particle A is projected with an initial velocity of 60 m/s. at an an...
Text Solution
|