Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
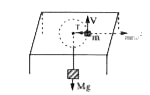
- In the Fig, shown below with what angular speed ' omega ' must 'm' wit...
Text Solution
|
- A disc of mass M and radius r is rotating with an angular velocity ome...
Text Solution
|
- Find the angular momentum about the axis of rotation and kinetic energ...
Text Solution
|
- A body of mass m and radius r is rotated with angular velocity omega a...
Text Solution
|
- A solid cylinder of mass M and radius R rotates about its axis with an...
Text Solution
|
- If earth suddenly stop rotating , then the weight of an object of m...
Text Solution
|
- Find the angular momentum of a particle of mass m describing a circle ...
Text Solution
|
- A circular disc of mass m and radius r is rolling over a horizontal ta...
Text Solution
|
- R = m (g - a) : R < W : : : R - W
Text Solution
|