A
B
C
D
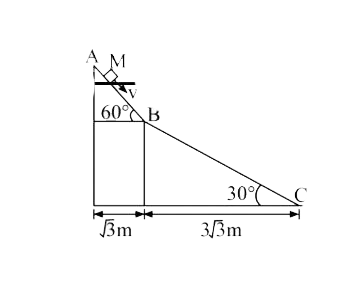
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- A small block of mass M move on a frictionless surface of an inclimed...
Text Solution
|
- A small block of mass M move on a frictionless surface of an inclimed ...
Text Solution
|
- A small block of mass M move on a frictionless surface of an inclimed ...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- A particle of mass m is projected up from the bottom of an inclined pl...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|
- A small block of mass M moves on a friction-less surface of an incline...
Text Solution
|
- A small block of mass M moves on a frictionless surface of an inclined...
Text Solution
|