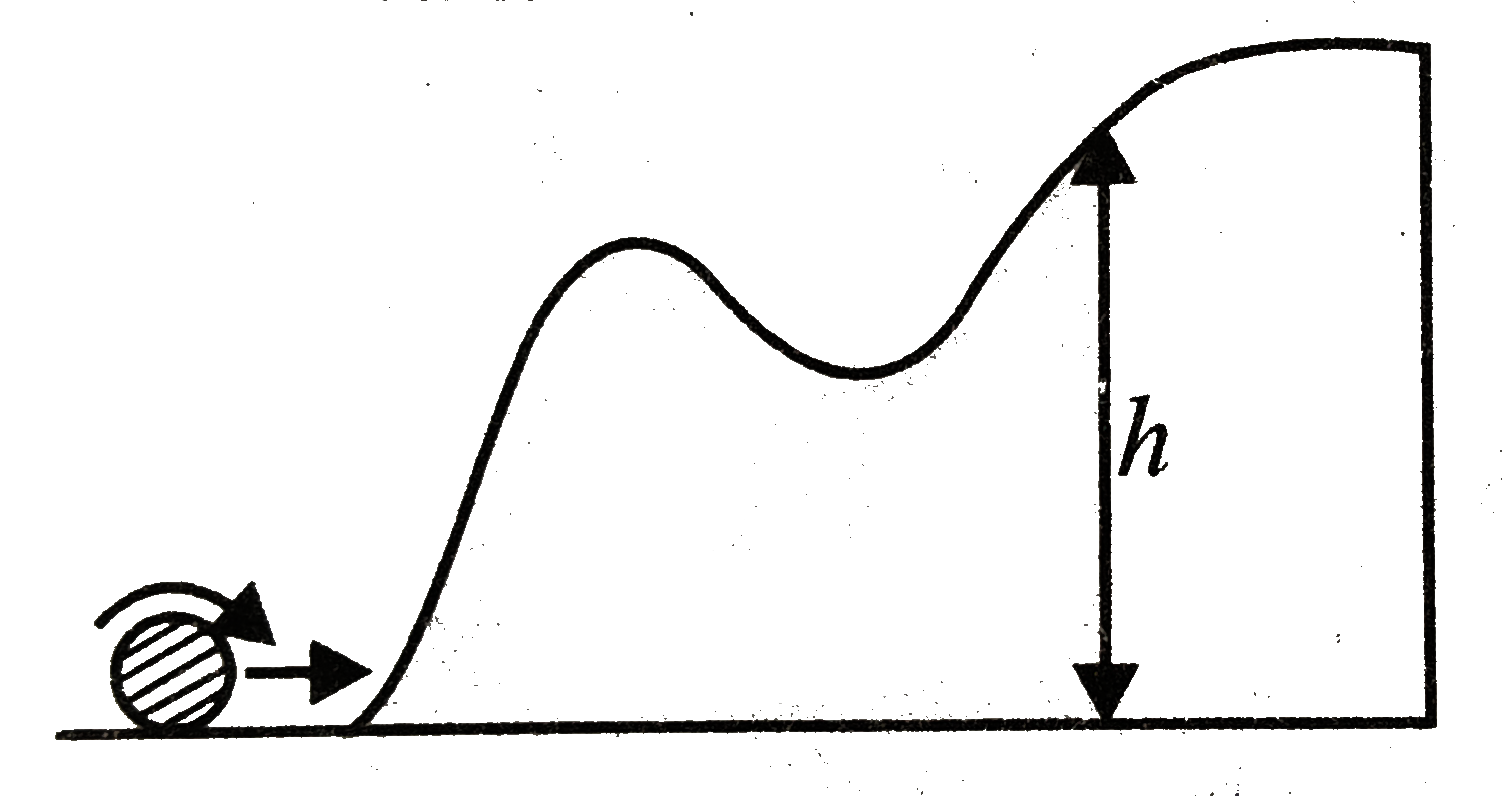
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A body of mass M and radius r, rolling on a smooth horizontal floor wi...
Text Solution
|
- A body of mass M and radius r, rolling on a smooth horizontal floor wi...
Text Solution
|
- A body of radius R and mass m is rolling smoothly with speed v on a ho...
Text Solution
|
- द्रव्यमान M तथा त्रिज्या R का एक पिण्ड क्षैतिज तल पर बिना फिसले चाल v ...
Text Solution
|
- An object of radius R and mass M is rolling horizontally without slipp...
Text Solution
|
- M द्रव्यमान तथा r त्रिज्या की वस्तु v वेग से एक क्षैतिज चिकने तल पर लु...
Text Solution
|
- A body of mass .m. and radius .r. rolling on a horizontal floor with v...
Text Solution
|
- A body of mass .m. and radius .r. rolling on a horizontal floor with v...
Text Solution
|
- An object of radius R and mass M is rolling horizontally without slipp...
Text Solution
|