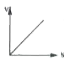
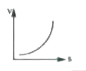
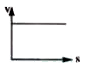
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A body falls from height h. The v-s graph is :
Text Solution
|
- A body is falling from a height h. After it has fallen a height (h)/(2...
Text Solution
|
- A body is falling from a height h. After it has fallen a height (h)/(2...
Text Solution
|
- स्वतंत्रतापूर्वक v वेग से h ऊँचाई से गिरते हुए पिण्ड के लिए v = sqrt(2...
Text Solution
|
- A body is falling from a height h. After it has fallen a height (h)/(2...
Text Solution
|
- A particle falls from a height h and rebounds to a height h (1) ( h (1...
Text Solution
|
- A body freely falling from a height h describes (7h)/16 in the last se...
Text Solution
|
- A body freely falling from a height h describes (11h)/36 in the last...
Text Solution
|
- A body freely falling from a height h describes (7h)/16 in the last se...
Text Solution
|