Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
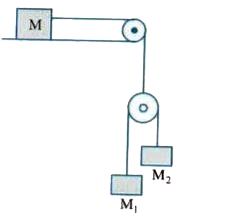
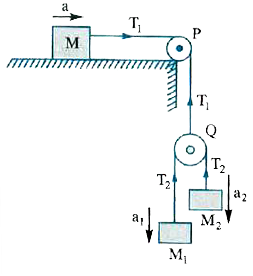
- Referring to figure calculate the downward acceleration of mass m1. As...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|
- Find the acceleration of the block of mass m. Assume pulleys are massl...
Text Solution
|
- In the systems shown in figure (A), (B), (C) and (D), the scales of th...
Text Solution
|
- In the systems shown in figure (A), (B), (C) and (D), the scales of th...
Text Solution
|
- In the systems shown in figure (A), (B), (C) and (D), the scales of th...
Text Solution
|
- In the systems shown in figure (A), (B), (C) and (D), the scales of th...
Text Solution
|
- Two blocks 'A' and 'B' having masses m(A) and m(a) , respectively are ...
Text Solution
|
- Referring to figure calculate the downward acceleration of mass m1. As...
Text Solution
|