Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
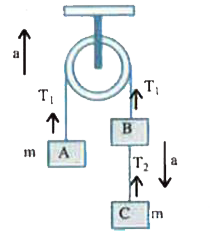
- Three equal weights of mass m each are hanging on a string passing ove...
Text Solution
|
- Three equal weight A,B and C of mass 2kg each are hanging on a string ...
Text Solution
|
- Three weights are hanging over a smooth fixed pulley as shown in the f...
Text Solution
|
- Three equal weights of mass m each are hanging on a string passing ove...
Text Solution
|
- Three equal weights of mass 3 kg each are hanging on a string passing ...
Text Solution
|
- Three equal weights of mass 2 kg each are hanging on a string passing ...
Text Solution
|
- Figure shows three blocks of mass m each hanging on a string passing o...
Text Solution
|
- Three equal weights of mass m each are hanging on a string passing ove...
Text Solution
|
- Figure shows three blocks of mass m each hanging on a string passing o...
Text Solution
|