Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
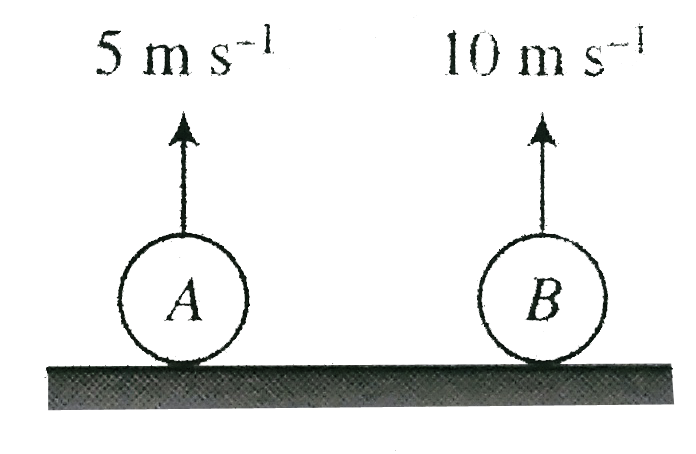
- Two particles A and B are thrown vertically upward with velocity, 5 m...
Text Solution
|
- Two particles A and B are thown vertically upward with velocity, verti...
Text Solution
|
- Find the maximum height reached by a particle which is thrown vertical...
Text Solution
|
- A particle is thrown vertically upward. Its velocity at half of the he...
Text Solution
|
- A particle is thrown with a velocity of u m/s. It passes A and B as sh...
Text Solution
|
- A particle is thrown with a velocity of u m/s. it passes A and B as sh...
Text Solution
|
- A particle is thrown vertically upwards its velocity at half o...
Text Solution
|
- A and B are thrown vertivally upward with velocity 5m/s and 10 m/s res...
Text Solution
|
- A pebble thrown vertically upwards with an initial velocity 50 m s^(-1...
Text Solution
|
 .
.