Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
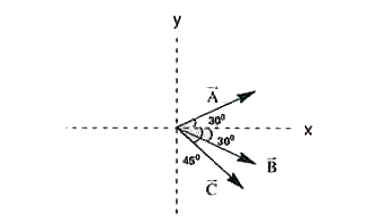
- Three vectors vecA, vecB, vecC are shown in the figure. Find angle bet...
Text Solution
|
- Three vectors vecA,vecB,vecC are shown in the figure. Find angle betwe...
Text Solution
|
- vecA, vecB and vecC are vectors such that vecC= vecA + vecB and vecC...
Text Solution
|
- If three unit vectors veca, vecb and vecc " satisfy" veca+vecb+vecc= v...
Text Solution
|
- If veca , vecb and vecc are three vectors such that vecaxx vecb =vecc...
Text Solution
|
- सिद्ध करें कि (i) [veca+vecb" "vecb+vecc" "vecc+veca]=2[veca" "v...
Text Solution
|
- If veca,vecb,vecc are three vectors such that veca+2vecb+vecc=vec0 and...
Text Solution
|
- Vectors vecA,vecB and vecC are shown in figure. Find angle between (i)...
Text Solution
|
- If veca , vecb , vecc are three vectors, prove that [veca+ve...
Text Solution
|