Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
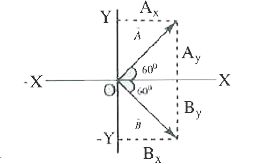
- Vector vecA is 2 cm long and is 60° above the x - axis in the first q...
Text Solution
|
- Vector vec(A) is 2 cm long and is 60^(@) above the x-axis in the first...
Text Solution
|
- If |veca+vecb|=60,|veca-vecb|=40 and |veca|=22 then find |vecb|.
Text Solution
|
- Let veca and vecb are two vectors inclined at an angle of 60^(@) , I...
Text Solution
|
- vectors veca and vecb are inclined at an angle theta = 60^(@). " If "...
Text Solution
|
- सदिश veca तथा vecb सरीख नहीं हैं| यह ज्ञात करें x के किस मान के लिए सद...
Text Solution
|
- If veca and vecb are two vectors of magnitude 2 and inclined at an ang...
Text Solution
|
- If |veca + vecb| =60 |veca-vecb|=40 and |vecb| = 46 find |veca|
Text Solution
|
- If veca and vecb are two vectors of magnitude 2 and inclined at an ang...
Text Solution
|