Home
Class 11
PHYSICS
A thin rod of length L is lying along th...

A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as `k((x)/(L))^n` where n can be zero or any positive number. If the position `X_(CM)` of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of `X_(CM)` on n?

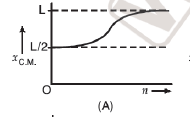
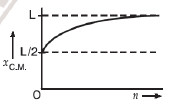
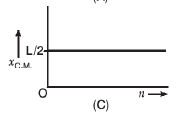
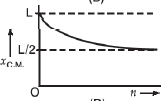
A


B


C


D


Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • Moment of Inertia

    MODERN PUBLICATION|Exercise Example|323 Videos

  • Gravitational potential and potential energy

    MODERN PUBLICATION|Exercise Exercise|17 Videos

  • Motion of Satellites

    MODERN PUBLICATION|Exercise Exercise|25 Videos

Similar Questions

Explore conceptually related problems

The density of a non-uniform rod of length 1 m is given by rho (x) = a (1 + bx^2) where a and b are constant and 0 le x le 1 . The center of mass of the rod will be at

A rod of length 12 cm moves with its ends alwaystouching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.

The coefficient of x^n , where n is any positive integer, in the expansion of (1+2x+3x^2 +... to oo)^(1//2) is:

A rod of length 12 cm moves with its ends always touching the coordinates axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end-in contact with x-axis.

Differentiate the following w.r.tx: l_n(Sec x + tanx)

For a linear plot of log (x/m) versus log P in a Freundlich adsorption isotherm, which of the following statement is correct? (k and n are constants).

The figure shows a right triangle with its hypotenuse OB along the y -axis and its vertex A on the parabola y=x^(2) . Let h represents the length of the hypotenuse which depends on the x -coordinate of the point A . The value of lim_(t to o (h) is equal to

lim_(x->0) (sin(nx)((a-n)nx – tanx))/x^2= 0 , when n is a non-zero positive integer, then a is equal to

Let f(x) be periodic and k be a positive real number such that f(x+k)+f(x)=0fora l lx in Rdot Prove that f(x) is periodic with period 2kdot

Let L= lim_(nrarr infty) int_(a)^(infty)(n dx)/(1+n^(2)x^(2)) , where a in R, then L can be

MODERN PUBLICATION-Moment of Inertia-Example
  1. A circular disc of radius R is removed from a bigger circular dise of ...

    Text Solution

    |

  2. Two spherical bodies of mass M and 5 M and radii R and 2 R respectivel...

    Text Solution

    |

  3. A thin rod of length L is lying along the x-axis with its ends at x = ...

    Text Solution

    |

  4. If vecA xx vecB = vecB xx vecA, then the angle between vecA and vevB i...

    Text Solution

    |

  5. A force of -F hatk acts on O, the origin of the coordinate system.The ...

    Text Solution

    |

  6. If vec F is the force acting in a particle having position vector vec ...

    Text Solution

    |

  7. Angular momentum of the particle rotating with a central force is cons...

    Text Solution

    |

  8. A particle performing uniform circular motion gas angular momentum L. ...

    Text Solution

    |

  9. A 'T' shaped object with dimensions shown in the figure, is lying on a...

    Text Solution

    |

  10. Four point masses, each of mass M, are placed at the corners of a squa...

    Text Solution

    |

  11. Consider a uniform square plate of side a and mass M. The moment of in...

    Text Solution

    |

  12. For a given uniform square lamina ABCD, whose centre is 0,

    Text Solution

    |

  13. Moment of inertia of a circular wire of mass M and radius R about is i...

    Text Solution

    |

  14. A circular disc X of radius R is made from an iron plate of thickness ...

    Text Solution

    |

  15. The moment of inertia of a uniform semi-circular disc of mass M and ra...

    Text Solution

    |

  16. One solid sphere A and another hollow sphere B are of same mass and sa...

    Text Solution

    |

  17. A solid sphere is rotating in free space. If the radius of the sphere ...

    Text Solution

    |

  18. A thin circular ring of mass M and radius R is rotating about its axis...

    Text Solution

    |

  19. A thin uniform rod of length I and mass m is swinging freely about a h...

    Text Solution

    |

  20. A thin circular ring of mass M and radius R is rotating about its axis...

    Text Solution

    |