Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
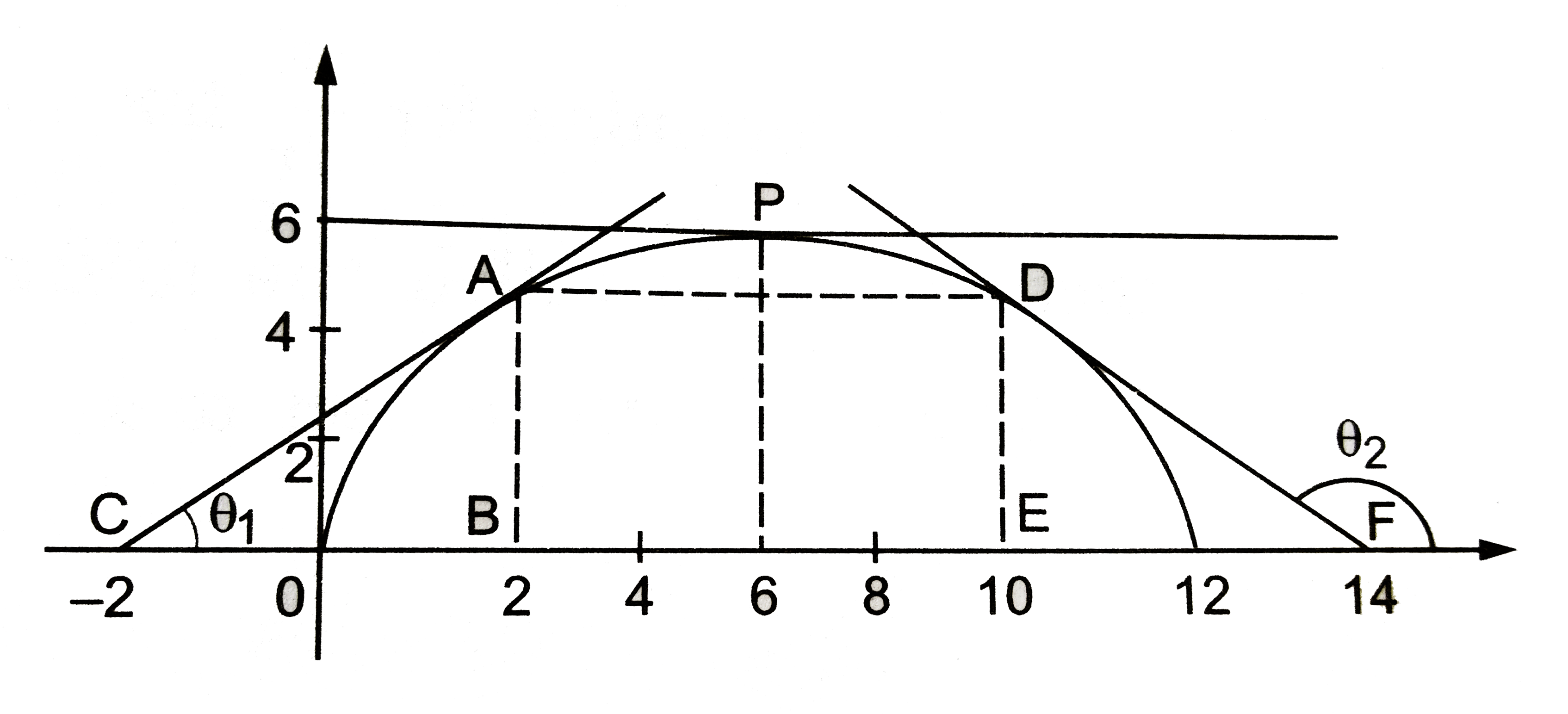
- From the curve given in figure find dy/dx at x=2, 6 and 10.
Text Solution
|
- From the curve given in figure find dy/dx at x=2, 6 and 10.
Text Solution
|
- If (dy)/(dx) =2x^(2) - 3 at any point (x,y) on a curve , find the equ...
Text Solution
|
- The gradient of the curve is given by (dy)/(dx)=2x-(3)/(x^(2)). The ...
Text Solution
|
- वक्र x^(2) = y के बिंदु (1,1) पर (dy)/(dx) का मान ज्ञात करें ।
Text Solution
|
- Find (dy)/(dx) as a function of x y = (x/2 - 1)^(-10)
Text Solution
|
- find dy/dx, y=10^((10^(x)))
Text Solution
|
- Find (dy)/(dx) for the curve x^(2)=y at the point (1, 1).
Text Solution
|
- Given (dy)/(dx) is directly proportional to the square of x and (dy)/(...
Text Solution
|