A swimmer can swim in still water at a rate 4.0 km/h. If he swims in a river flowing at 3.0 km/h and keeps his direction (with respect to water) perpendicular to the current, find his velocity with respect to the ground.
A swimmer can swim in still water at a rate 4.0 km/h. If he swims in a river flowing at 3.0 km/h and keeps his direction (with respect to water) perpendicular to the current, find his velocity with respect to the ground.
Text Solution
Verified by Experts
The velocityf the swimmer with respect to water is `vecv_(S,R)=4.0 km/h` in the direction respect to the ground is `vecv_(R,G)=3.0 km/h` along the length of the river. The velocity of the swimmer with respect to the ground is `vec_(S,G)` where
`vecv_(S,G)=vecv_(S,R)+vecv_(R,G)`
ure shows the velocities. It is clear that,
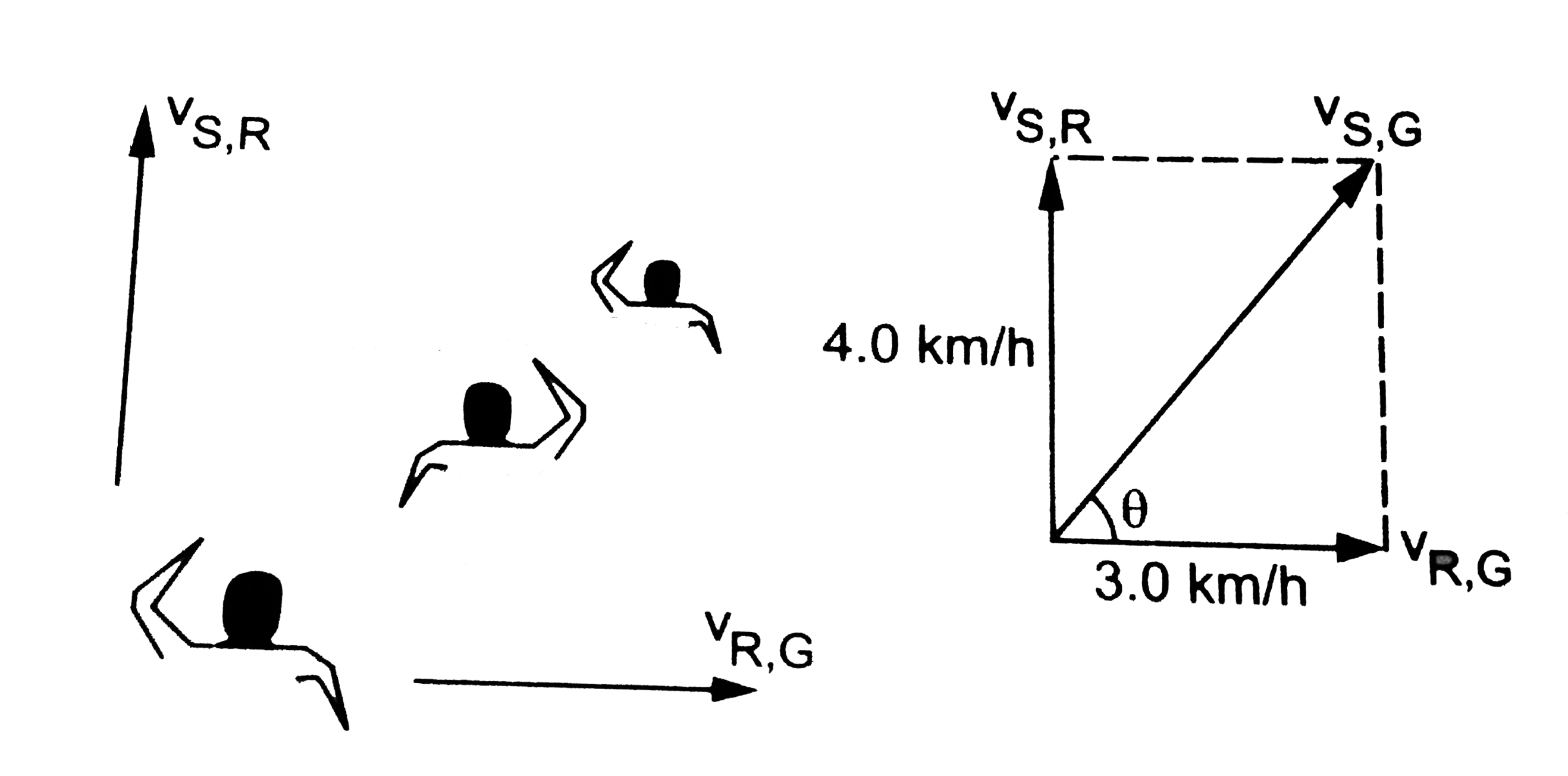
`v_(S,G)=sqrt((4.0 km/h)^2+(3.0 km/h)^2)`
`=5.0 km/h`
The angle theta made with the diection of flow is
`tan theta=(4.0 km/h)/(3.0 km/h)=4/3`
`vecv_(S,G)=vecv_(S,R)+vecv_(R,G)`
ure shows the velocities. It is clear that,
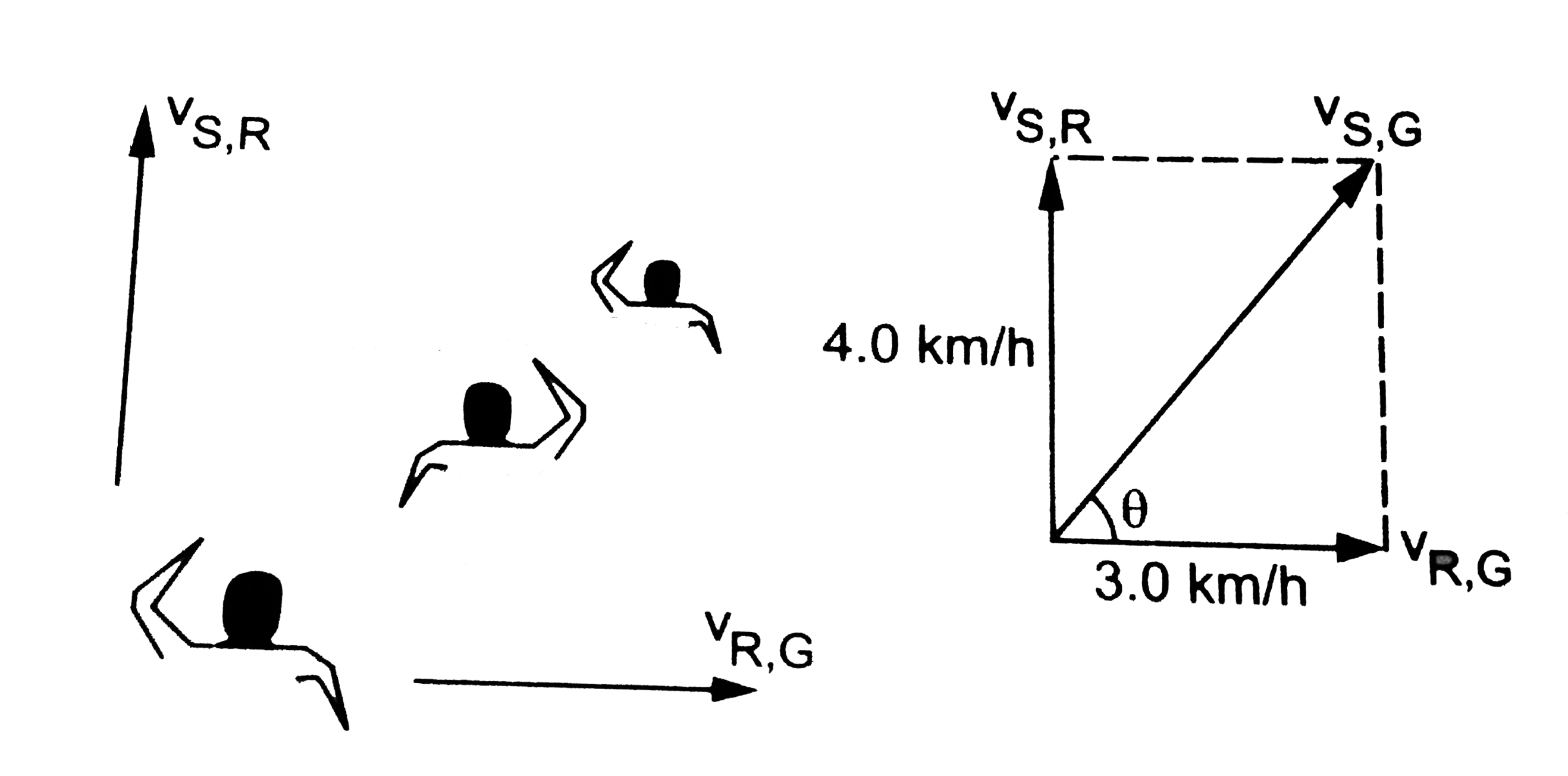
`v_(S,G)=sqrt((4.0 km/h)^2+(3.0 km/h)^2)`
`=5.0 km/h`
The angle theta made with the diection of flow is
`tan theta=(4.0 km/h)/(3.0 km/h)=4/3`
Similar Questions
Explore conceptually related problems
A river 400 m wide is flowing at a rate of 2.0 m//s. A boat is sailing at a velocity of 10.0 m//s with respect to the water In a direction perpendicular to the river. (a) Find the time taken by the boat to reach the opposite bank. (b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
A man can swim with a speed of 4.0 km/h in still water . How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river current ? How far down the river does he go when he reaches the other bank ?
A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. A conveyer belt of width D is moving along x-axis with velocity V. A man moving with velocity U on the belt in the direction perpedicular to the belt's velocity with respect to belt want to cross the belt. The correct expression for the drift (S) suffered by man is given by (k is numerical costant )
A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T), S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. From the concept of directed dimension what is the formula for a range (R) of a cannon ball when it is fired with vertical velocity component V_(y) and a horizontal velocity component V_(x) , assuming it is fired on a flat surface. [Range also depends upon acceleration due to gravity , g and k is numerical constant]
A physical quantity is a phyical property of a phenomenon , body, or substance , that can be quantified by measurement. The magnitude of the components of a vector are to be considered dimensionally distinct. For example , rather than an undifferentiated length unit L, we may represent length in the x direction as L_(x) , and so forth. This requirement status ultimately from the requirement that each component of a physically meaningful equation (scaler or vector) must be dimensionally consistent . As as example , suppose we wish to calculate the drift S of a swimmer crossing a river flowing with velocity V_(x) and of widht D and he is swimming in direction perpendicular to the river flow with velocity V_(y) relation to river, assuming no use of directed lengths, the quantities of interest are then V_(x),V_(y) both dimensioned as (L)/(T) , S the drift and D width of river both having dimension L. with these four quantities, we may conclude tha the equation for the drift S may be written : S prop V_(x)^(a)V_(y)^(b)D^(c) Or dimensionally L=((L)/(T))^(a+b)xx(L)^(c) from which we may deduce that a+b+c=1 and a+b=0, which leaves one of these exponents undetermined. If, however, we use directed length dimensions, then V_(x) will be dimensioned as (L_(x))/(T), V_(y) as (L_(y))/(T) , S as L_(x)" and " D as L_(y) . The dimensional equation becomes : L_(x)=((L_(x))/(T))^(a) ((L_(y))/(T))^(b)(L_(y))^(c) and we may solve completely as a=1,b=-1 and c=1. The increase in deductive power gained by the use of directed length dimensions is apparent. Which of the following is not a physical quantity
A swimmer swins in still water at a speed =5 km//hr . He enters a 200m wide river, having river flow speed =4km//hr at point A and proceeds to swim at an angle of 127^(@) (sin 37^(@) = 0.6) with the river flow direction. Another point B is located directly across A on the other side. the swimmer lands on the other bank at a point C , form which he walks the distance CB with a speed = 3km//hr . The total time in which he reaces from A to B is
A boat is moving with a velocity 3 hat i+ 4hat j with respect to ground. The water in the river is moving with a velocity -3 hat i - 4 hat j with respect to ground. The relative velocity of the boat with respect to water is.
A boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east. (a) In which direction must it be steered to cross the river perpendicular to current ? (b) How long will it take to cross the river in a direction perpendicular to the river flow ? (c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
A man can swim at a speed 2ms^(-1) in still water. He starts swimming in a river at an angle 150^(@) with direction of flow of water and reaches at the exactly oppsite point on the opposite bank. (a) Find the speed of flowing water. (b) If width of river is 1 km then calculate the time taken also
A man is crossing a river flowing with velocity of 5m//s . He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
Recommended Questions
- A swimmer can swim in still water at a rate 4.0 km/h. If he swims in a...
Text Solution
|
- A swimmer can swim in still water at a rate 4.0 km/h. If he swims in a...
Text Solution
|
- A man can swim at the rate of 5 kmh^(-1) in still water A. One km wide...
Text Solution
|
- A man wishes to swim across a river 0.5km. wide if he can swim at the...
Text Solution
|
- A man desires to swim across the river in shortest time. The velocity ...
Text Solution
|
- एक नदी का जल 5 किमी/घंटा की चाल की चाल से बह रहा है एक व्यक्ति जो जल क...
Text Solution
|
- एक व्यक्ति नदी में जल कि धारा की दिशा तथा धारा के विपरीत दिशा में 25 ...
Text Solution
|
- एक तैराक स्थिर पानी में 4. 0 km/h की चल से तैर सकता है । वह 3. 0 km//...
Text Solution
|
- The stream of a river is flowing with a speed of 2 km/h. A swimmer can...
Text Solution
|