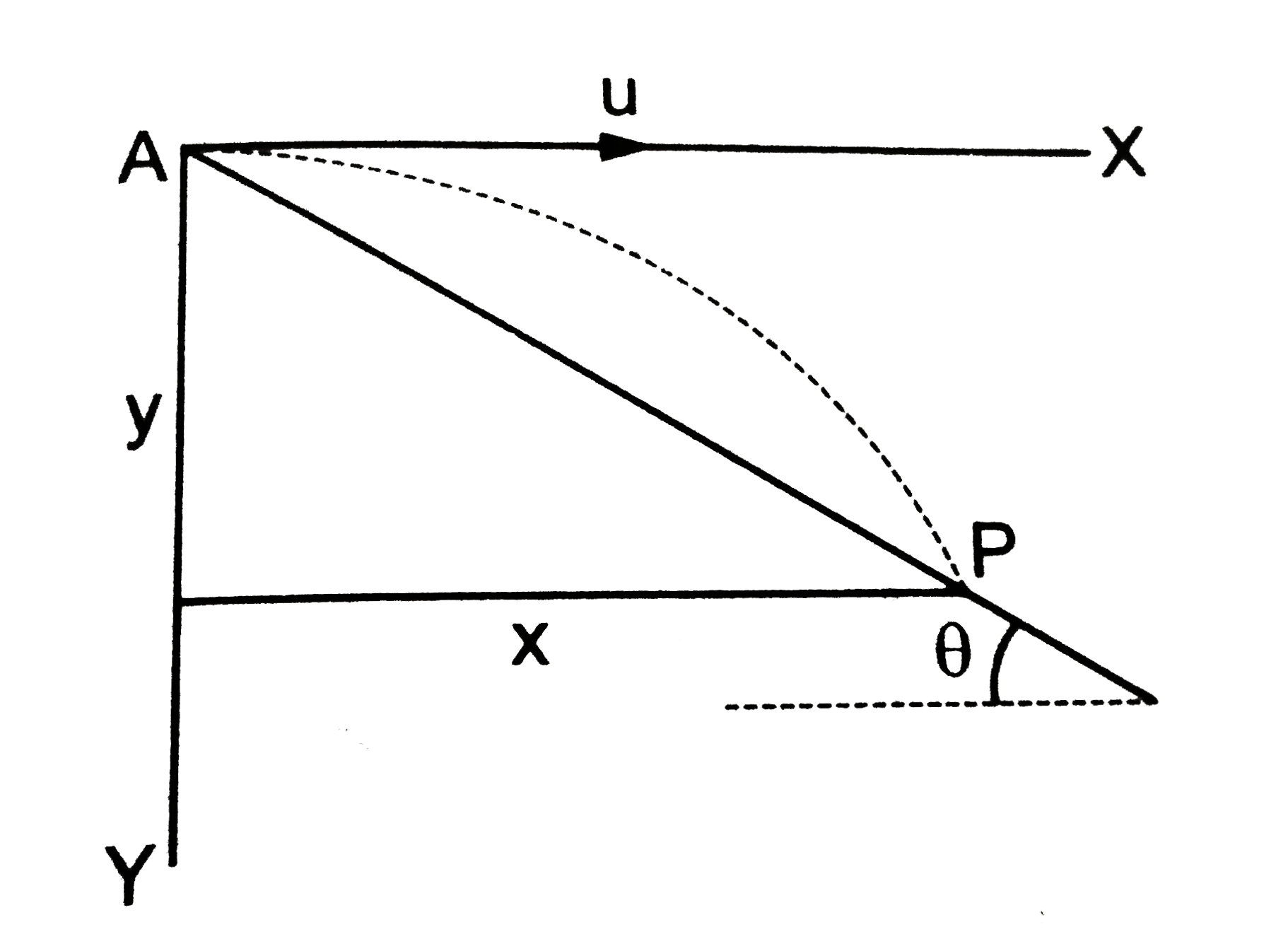
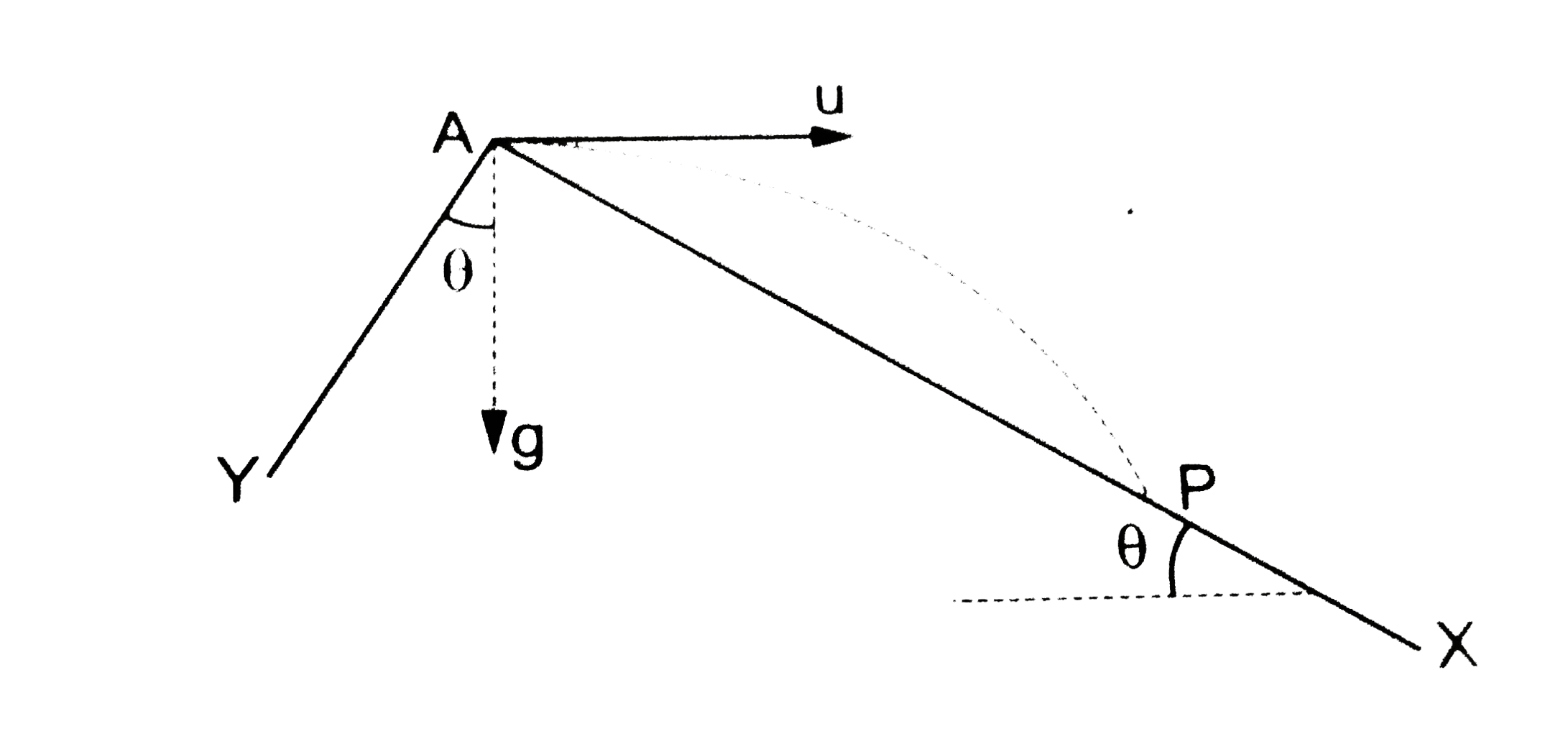
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is projected horizontally with a speed u from the top of pl...
Text Solution
|
- A ball is projected horizontally with a speed v from the top of the pl...
Text Solution
|
- A pariicle is projected horizontally with a speed (u) from top of a pl...
Text Solution
|
- A particle is projected horizontally with a speed u from the top of pl...
Text Solution
|
- A particle is projected horizontal with a speed u from the top of pla...
Text Solution
|
- A particle is projected horizontally with a speed V=5m/s from the top ...
Text Solution
|
- A particle is projected up an inclines plane. Plane is inclined at an ...
Text Solution
|
- A particle is thrown horizontally from the top of an inclined plane , ...
Text Solution
|
- A particle projected horizontally from the top of an inclined plane in...
Text Solution
|