Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A man can swim at a speed of 3 km/h in still water. He wants t cross a...
Text Solution
|
- A man can swim in still water ast a speed of 3 km/h. He wants to cross...
Text Solution
|
- A man can swim at a speed of 3 km/h in still water. He wants t cross a...
Text Solution
|
- A man can swim at a speed of 3 km h^-1 in still water. He wants to cro...
Text Solution
|
- A man can swim at a speed of 3 km h^-1 in still water. He wants to cro...
Text Solution
|
- A man can swim at a speed of 5km//h in the still water. He wants to cr...
Text Solution
|
- 2 km wide river flowing with a rate of 5 km/hr. A man can swim in the ...
Text Solution
|
- A man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1...
Text Solution
|
- A man can swim in still water at a speed of 6 kmph and he has to cross...
Text Solution
|
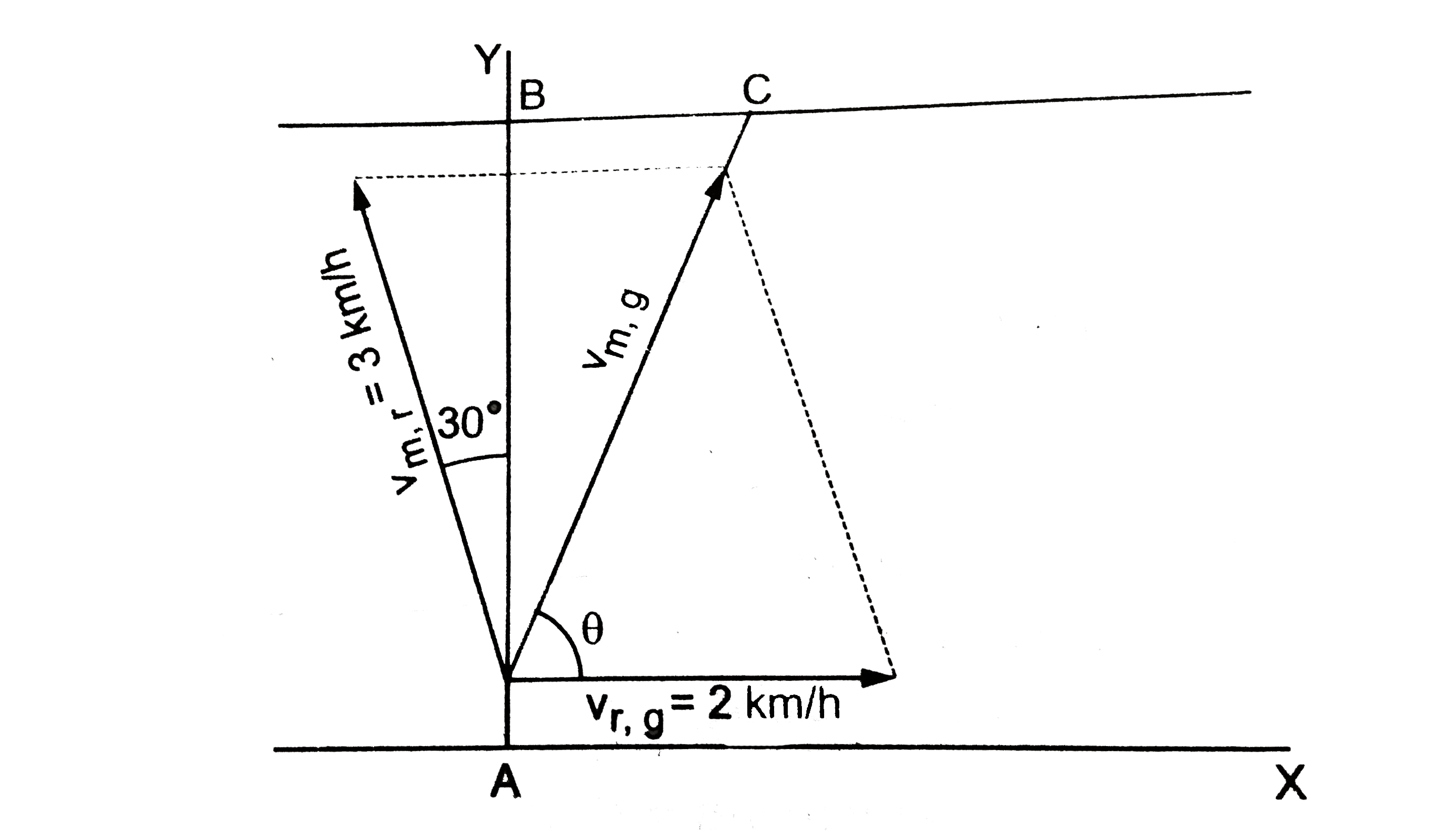 Here `vecv_(r,g)=` velocity of the river with respect to the ground
Here `vecv_(r,g)=` velocity of the river with respect to the ground