Similar Questions
Explore conceptually related problems
Recommended Questions
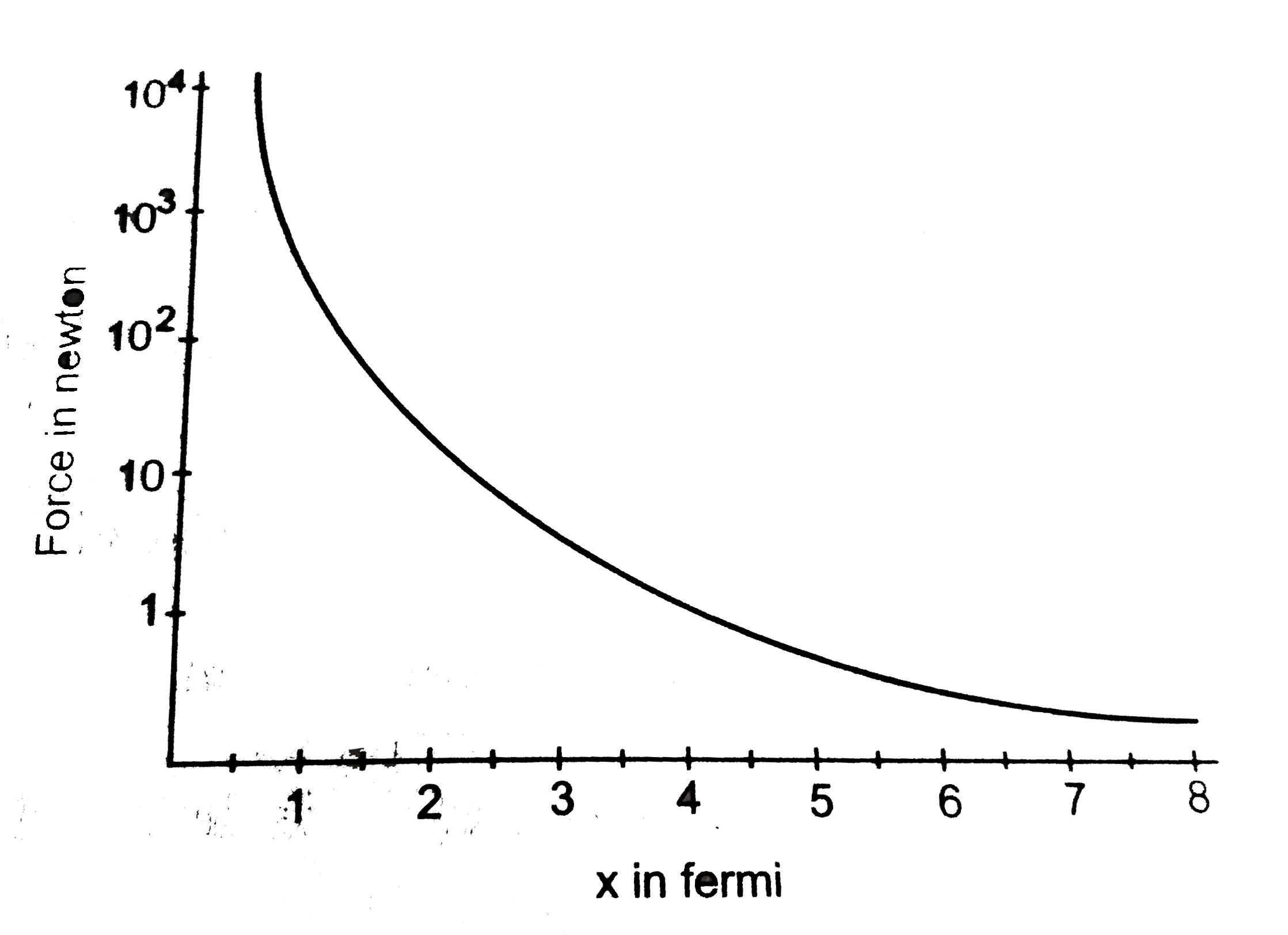
- Suppose the magnitude of Nuclear force between two protons varies with...
Text Solution
|
- Let F(pp), F(pn) and F(nn) denote the magnitudes of the nuclear force ...
Text Solution
|
- Let Fpp, Fpn and Fnn denote the magnitudes of the nuclear force by a p...
Text Solution
|
- What is varied in a FM wave?
Text Solution
|
- Consider the situation as shown in the figure. The system is free to m...
Text Solution
|
- The ration of coulomb force and nuclear force between two protons insi...
Text Solution
|
- Let F(PP),F(Pn) and F("nn") denote the magnitude of net force by a pro...
Text Solution
|
- Write down the advantages and limitations of frequency modulation (FM)...
Text Solution
|
- ""^(125)Fe का नाभिकीय व्यासार्ध क्या है यदि ""^(27)Al का 3.6 fm हो ?
Text Solution
|