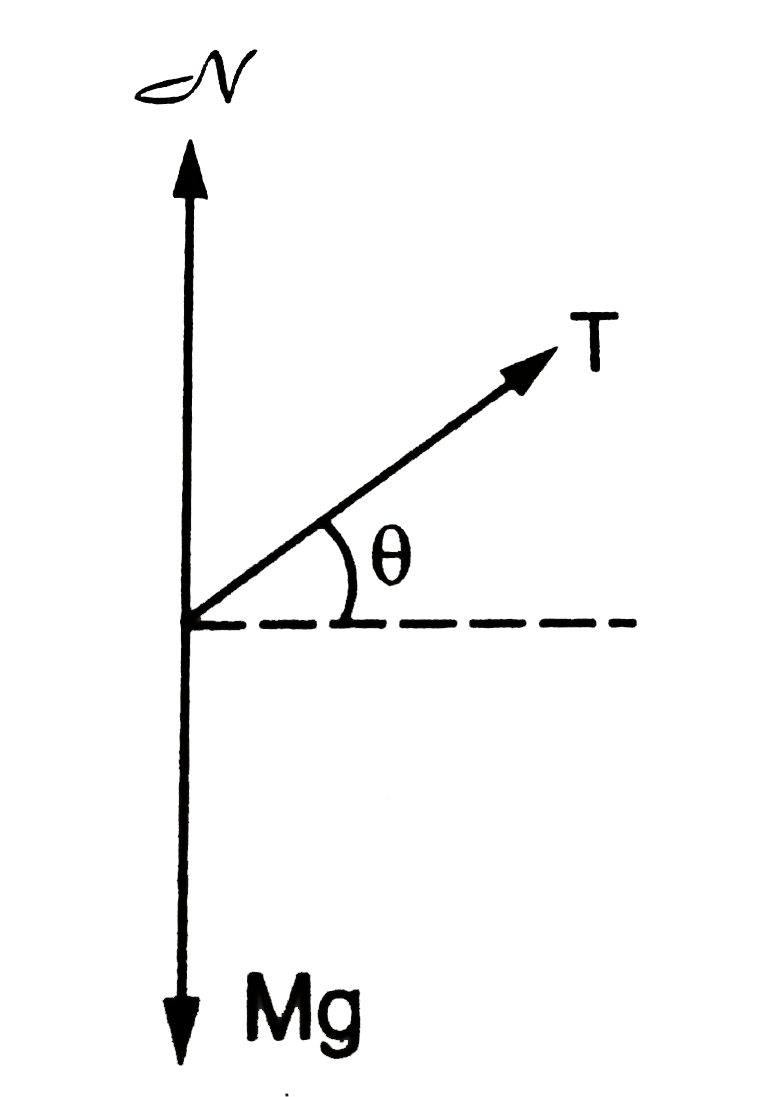
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block of mass M is pulled on a smooth horizontal table by a string m...
Text Solution
|
- A block of mass M is pulled on a smooth horizontal table by a string m...
Text Solution
|
- A constant force F=m2g/s is applied on the block of mass m1 as shown i...
Text Solution
|
- A block of mass m is placed on a horizontla surface. If the block is p...
Text Solution
|
- Two blocks of masses m and 2m are placed on a smooth horizontal surfac...
Text Solution
|
- In the system shown in the figure, all surfaces are smooth. Block A an...
Text Solution
|
- A wooden block of mass m resting on a rough horizontal table (coeffici...
Text Solution
|
- A 10 kg block kept on an inclined plane is pulled by a string applying...
Text Solution
|
- A book of mass 5 kg is kept on a horizontal table. It is connected to ...
Text Solution
|