Suppose the acceleration of `n_q1` is `a_0` towards right. That will also be the downward acceleration of the pulley B because the string connecting `m_1 and m_3` has a constant length. This implies tht the decrease i the separation between `m_2 and ` B equals the increase in teh separation between `m_3 and B.` So, the upward acceleeration of `m_2` wiht respect to B equals the downward acceleration of `m_3` with respect of B. Let this acceleration be `a`
The acceleration of `m_2` with respect to the ground `=a_0-a` (downward) and the acceleration of `m_3` with respect to the ground `=a_0+a` (downward).
These accelerations will be used in Newton's laws. Let the tension be T in the upper string and T' in the lower string. consider the motion of the pulley B.
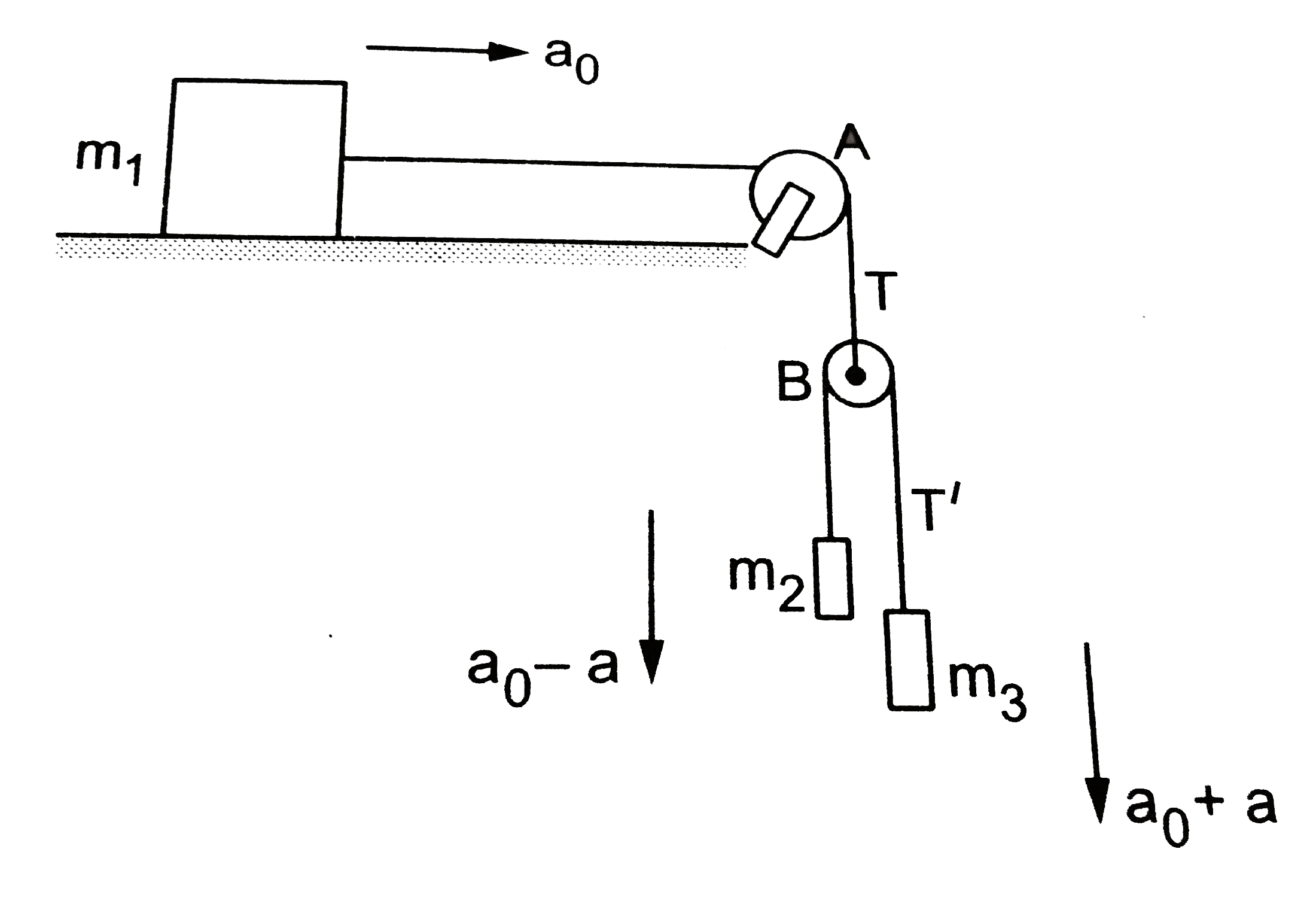
The forces on this light pulley are ltbr. a. T upward by the upper sting and
2T' downwards by thelower string.
As the mass of the pulley is negligible,
` 2T'-T=0`
giving `T-=T/2`............i
Motion `m_1`
THe acceleration is `a_0` in the horizontal direction. The forces on `m_1` are
a. T by the string (horizontal)
b. `m_1` g by theearth (verticlaly downwards) and
N by the table (verrtically upwards).
IN the horizontal direction the equation
`T=m_1a_0`
Motion of `m_2`: acceleration is `a_0-a` in the fownward direction. Teh forces on `m_2` are
a. `m_2g` downward by teh earth and
`T'=T/2` upward by teh string.
Thus, `m_2g-T/2=m_2(a_0+a)`...........iii
Moton of `m_3`= The aceeleration is `(a_0+a)` downward. The forces on `m_3` are
a. `m_3g` downward by the earth and
b. T'=T/2 upward by the string. thus,
`m_3g-T/2=m_3(a_0+0)`...........iv.
We want to calculate `a_0` so we shall elimiN/Ate T and a from ii, iii, and iv.
Putting T from ii in and iii and iv,
`a_0-a=(m_2-mI_1a_0/2)/m_2=g-(m_1a_0)/(2m_2)`
and `a_0+a+(m_3g-m-1a_0/2)/M_3 =g-(m_1 a_0)/(2m_3`
Adding `2a_0=2g-(m_1a_0)/2(1/m_2+1/m_3)`
`a_0=g-(m_1a_0)/4 (1/m_2+1/m_3)`
or, `a_0[1+m_1/4(1/m-2+1/m_3)]=g`
`or, a_0=g/(1+ m_1/4(1/m_2+1/m_3))`
