Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle slides down a smooth in clined plane of elevation theta fix...
Text Solution
|
- A particle slides down a smooth in clined plane of elevation theta fix...
Text Solution
|
- A block slides down from top of a smooth inclined plane of elevation ●...
Text Solution
|
- A particle slides down a smooth incline of inclination 37^(@) , fixed ...
Text Solution
|
- A particle slides down a smooth inclined plane of elevation , fixed i...
Text Solution
|
- A smooth inclined plane is inclined at an angle theta with the horizon...
Text Solution
|
- A particle slides down a smooth inclined plane of elevation theta fixe...
Text Solution
|
- A particle slides down on a smooth incline of inclination 30^(@) , fix...
Text Solution
|
- A smooth wedge with elevation theta is fixed in an elevator moving up...
Text Solution
|
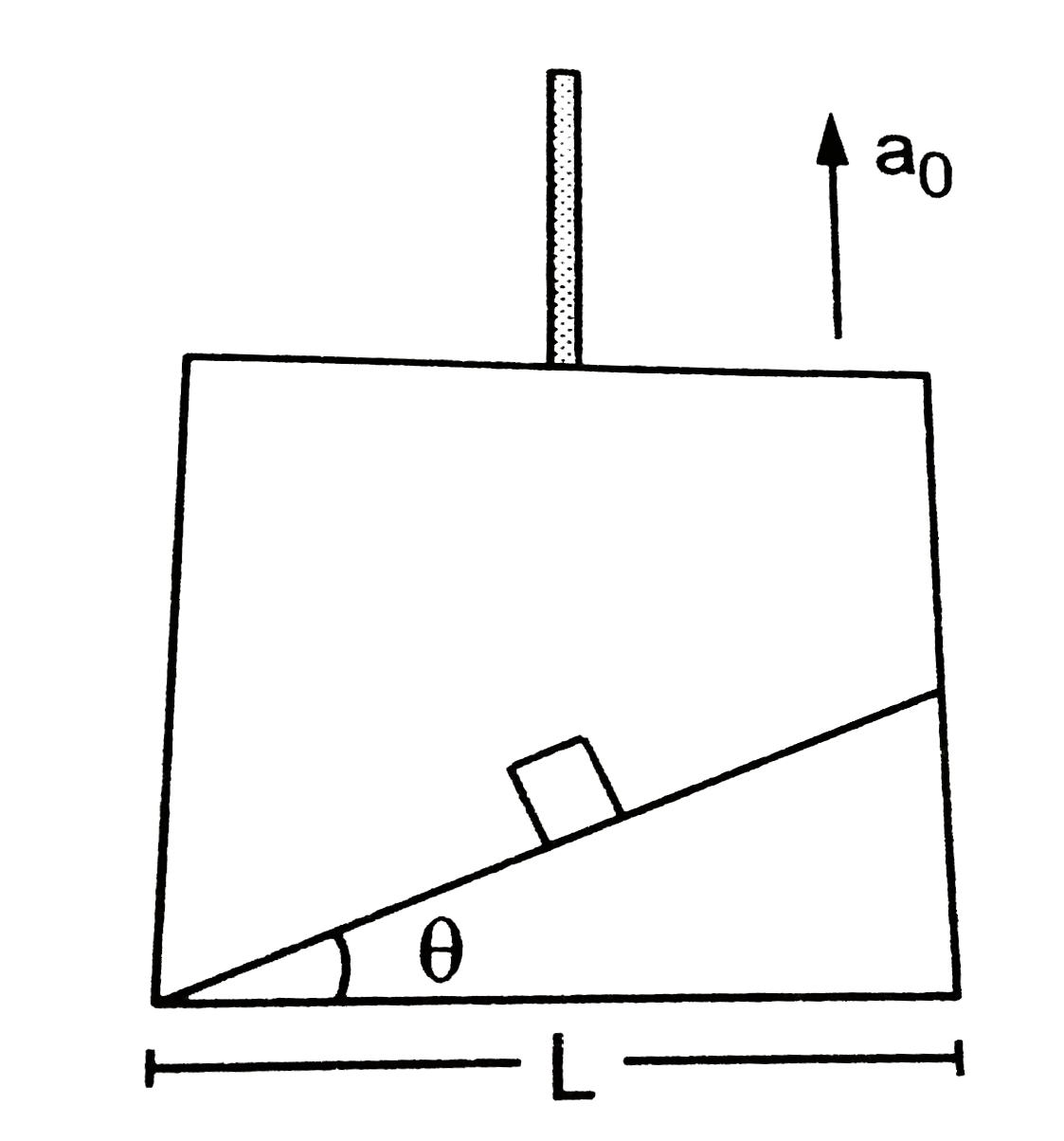
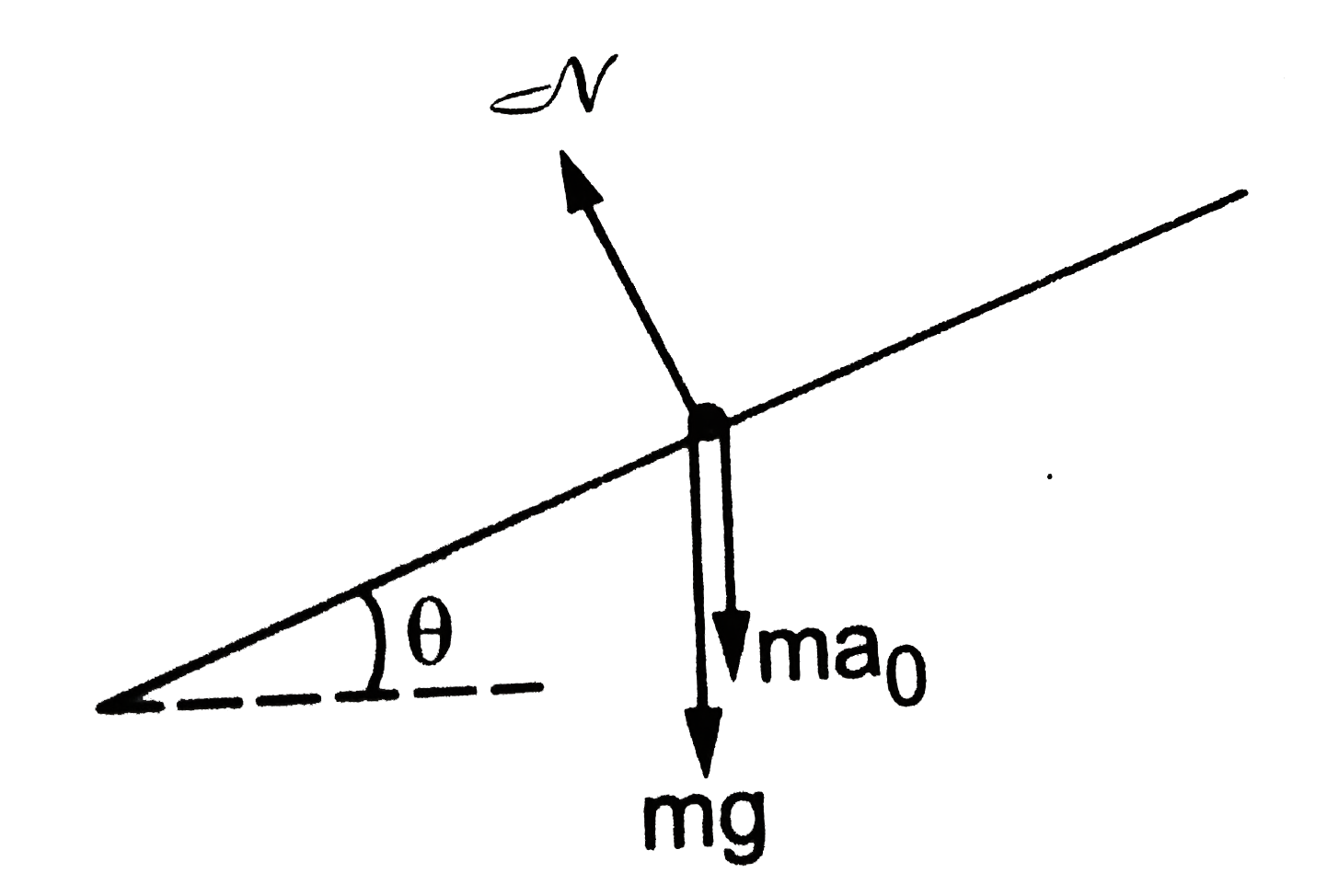 Let a be the acceleration of eth partice withrespect to the incline. Taking components of the forces paralel to the incline and applying Newton's law,
Let a be the acceleration of eth partice withrespect to the incline. Taking components of the forces paralel to the incline and applying Newton's law,