Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
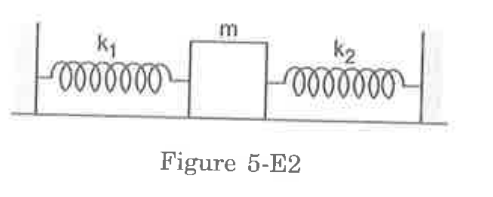
- Both the springs shown in figure are untretched. If the block is displ...
Text Solution
|
- Both the springs shown in figure are untretched. If the block is displ...
Text Solution
|
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A block of mass m is attached to the two springs in vertical plane as ...
Text Solution
|
- A block A of mass 2 kg is connected with two springs, as shown . The ...
Text Solution
|
- Consider the spring block system shown in the figure. Initially block ...
Text Solution
|
- चित्र में दिखाए गए दोनों स्प्रिंग अपनी स्वाभाविक लंबाई में हैं | यदि ब...
Text Solution
|