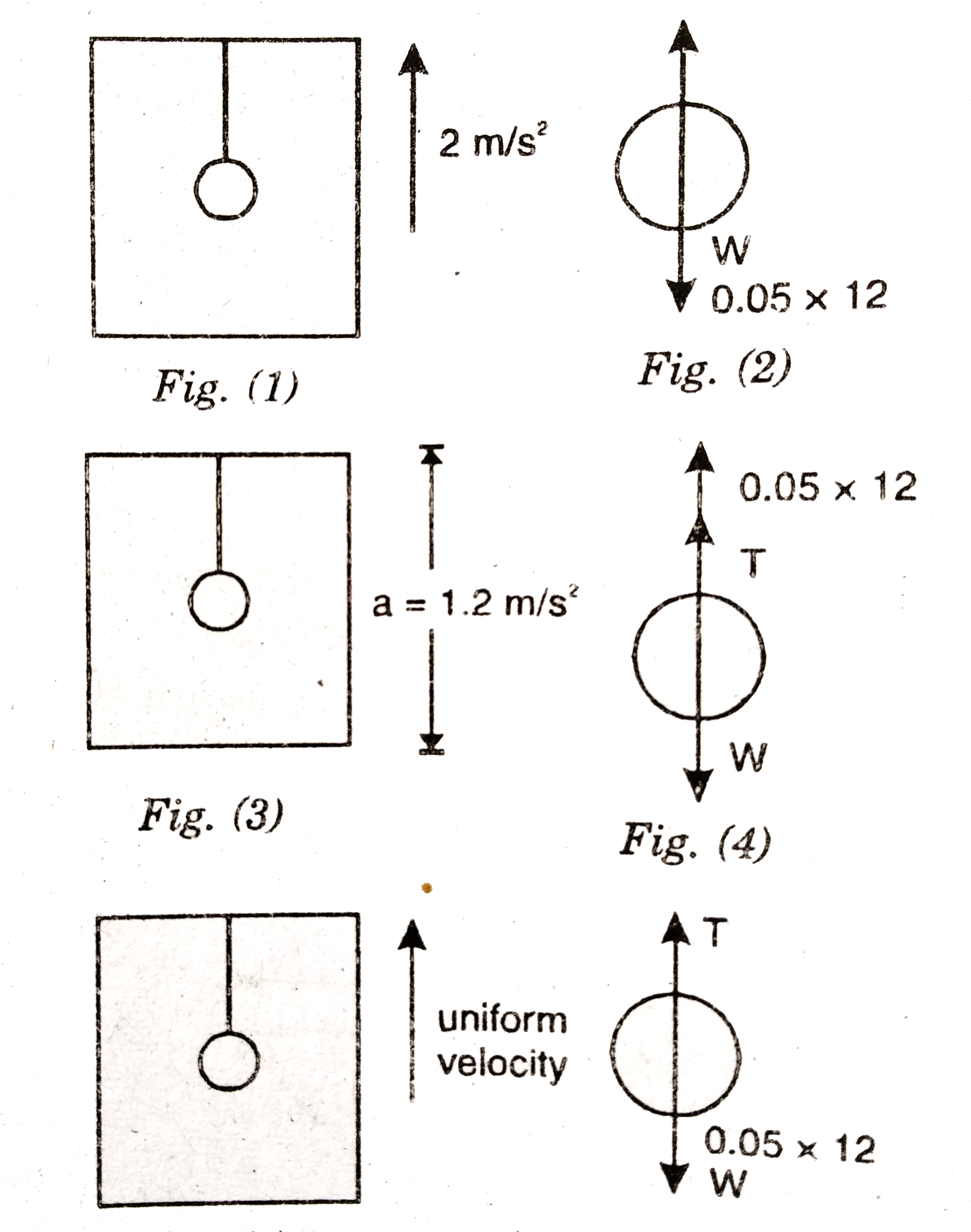
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- What is the value of the form factor for sinusoidal current? a) π/2 ...
Text Solution
|
- Extend the definition of the following by continuity f(x)=(1−cos7(x−π)...
Text Solution
|
- There exists a triangle A B C satisfying the conditions (A) bsinA = ...
Text Solution
|
- The value of lim(x to oo ) (log(e)(log(e)x))/(e^(sqrt(x))) is . (a) π...
Text Solution
|
- The angular speed of a motor wheel is increased from 1200 rpm to 3120 ...
Text Solution
|
- int(0)^(pi//2) sin 2x log (tan x) dx is equal to a) π b) π/2 c...
Text Solution
|
- The value of int0^1(8 log(1+x))/(1+x^(2)) dx is a) πlog2 b) π/8log...
Text Solution
|
- int(0)^(pi//2)(sin^(4)x)/(sin^(4)x + cos^(4)x)dx= (a) π (b) π/4 (...
Text Solution
|
- The area of the region bounded by the ellipse x^2/a^2+y^2/b^2=1 is………a...
Text Solution
|