Home
Class 11
PHYSICS
A cylindrical bucket filled with water i...

A cylindrical bucket filled with water is whirled around in a vertical circle of radius r. What can be the minimum speed at the top of the path if water does not all out from the bucket ? If it continues with this speed, what normal contact force the bucket exerts on water at the lowest point of the path?

Text Solution

Verified by Experts

consider water as the system. At the top of the cfircle its acceleration towards the centre is vertically downward with magnitude `v^2/r`. The forces on water asre ure.
a. weight Mg downward and
b. normal force by the bucket, aslso downward

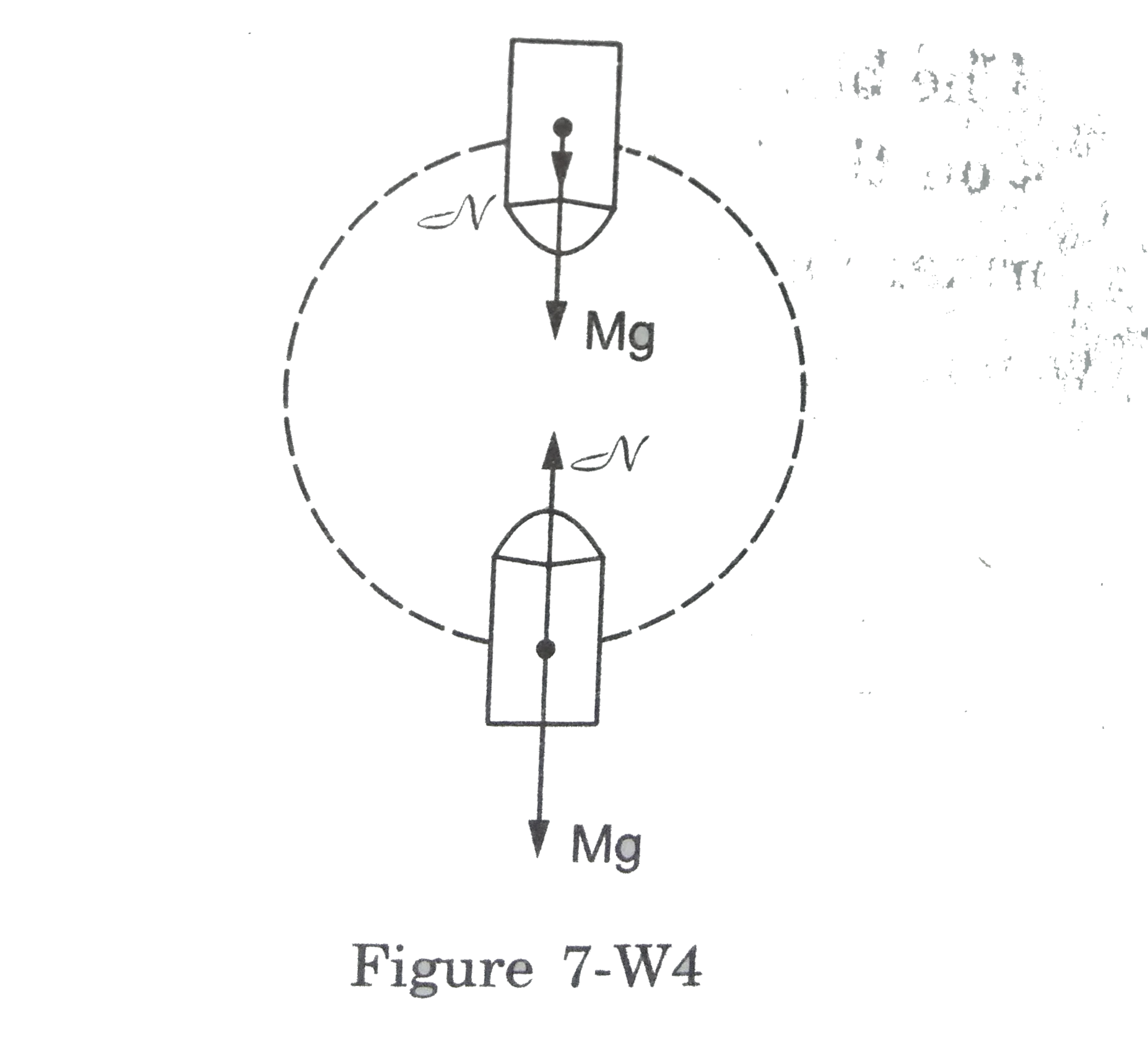
So, from Newton's second law
`Mg=N=Mv^2/r`
For water not to fall out from the bucket `Nge0`
Hence, `Mv^2/rgeMg or, v^2rarr=rg`
the minimum speed at the top must be `sqrt(rg)`
If the bucket continues on the circle with this minimum speed `sqrt(rg)` the forces at the bottom of theh path are
a. weight Mg downward and
b. normal contact force N by the bucket upward.
The acceleration is twoards the centre which is vertically upward, so
`N'-Mg=Mv^2/g`
`or, N'=M(g+v^2/r)=2Mg`
Promotional Banner

Similar Questions

Explore conceptually related problems

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given by

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The limiting electric potential of the sphere is

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. If the initial kinetic energy of a proton is 2.56 ke V , then the final potential of the sphere is

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The total energy (E) of a proton in the beam travelling with seed v at a distance of r (r ge R) from point O. Assuming that the sphere has acquired an electrostatic charge Q is

A car is moving along a banked road laid out as a circle of radius r . (a) What should be the banking angle theta so that the car travelling at speed v needs no frictional force from tyres to negotiate the turn ? (b) The coefficient of friction between tyres and road are mu_(s) = 0.9 and mu_(k) = 0.8 . At what maximum speed can a car enter the curve without sliding toward the top edge of the banked turn ?

You may have seen in a circus a motorcyclist driving in vertical loops inside a ‘deathwell’ (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m