Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
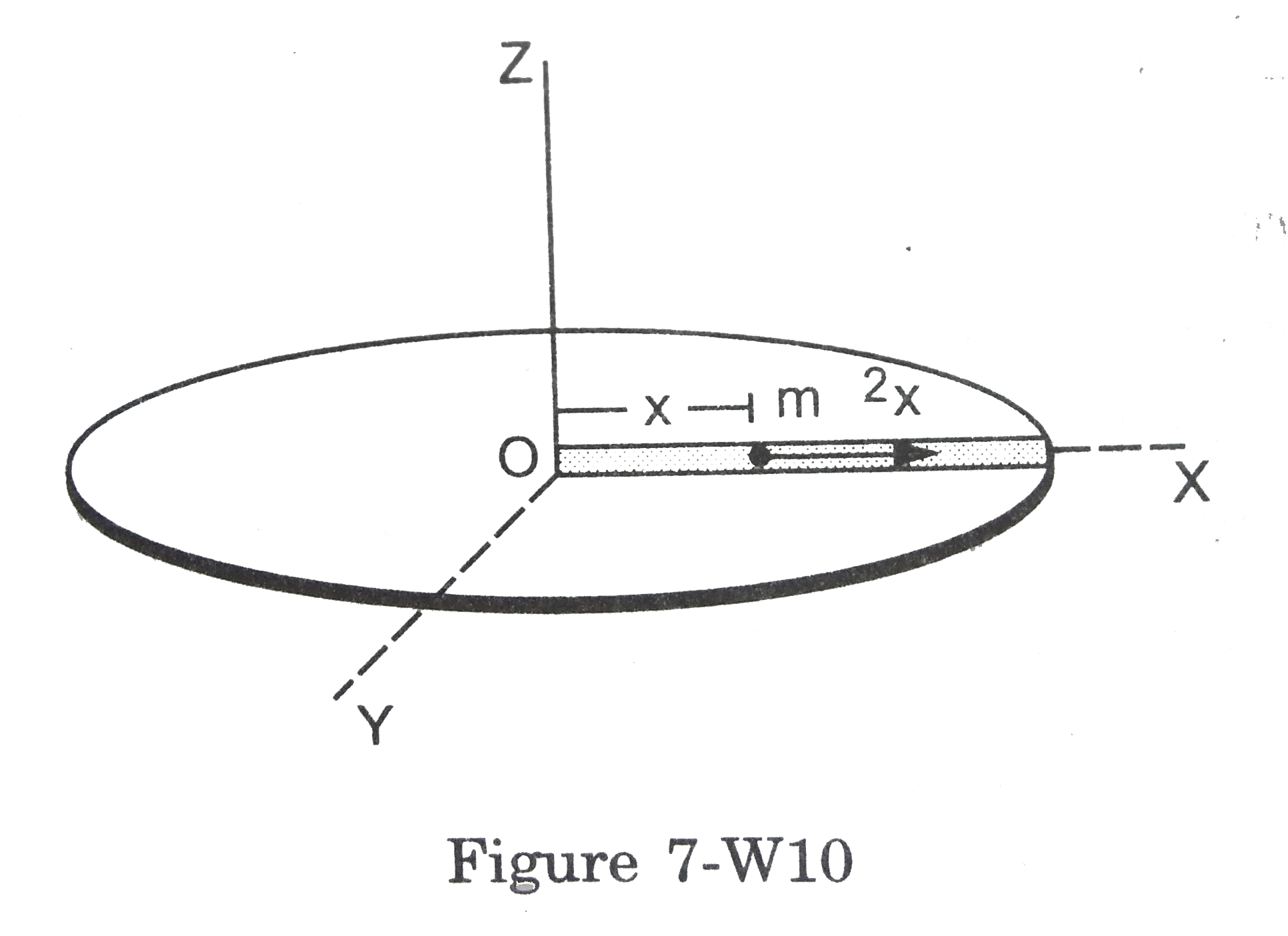
- A table with smooth horiztonal surface is truning at an angular speed ...
Text Solution
|
- A table with smooth horiztonal surface is truning at an angular speed ...
Text Solution
|
- A table with smooth horizontal surface is fixed in a cabin that rotate...
Text Solution
|
- A particle is moving at a constant speed V from a large distance towar...
Text Solution
|
- Figure shows a block A of mass 6 m having a smooth semicircular groove...
Text Solution
|
- A very small groove is made in the earth, and a particle of mass m(0) ...
Text Solution
|
- A particle moving on the inside of a smooth sphere of radius r describ...
Text Solution
|
- क्षैतिज सतह वाली एक वृत्ताकार टेबुल अपने अक्ष के परितः एकसमान कोणीय वे...
Text Solution
|
- A circular table with smooth horizontal surface is rotating at an angu...
Text Solution
|