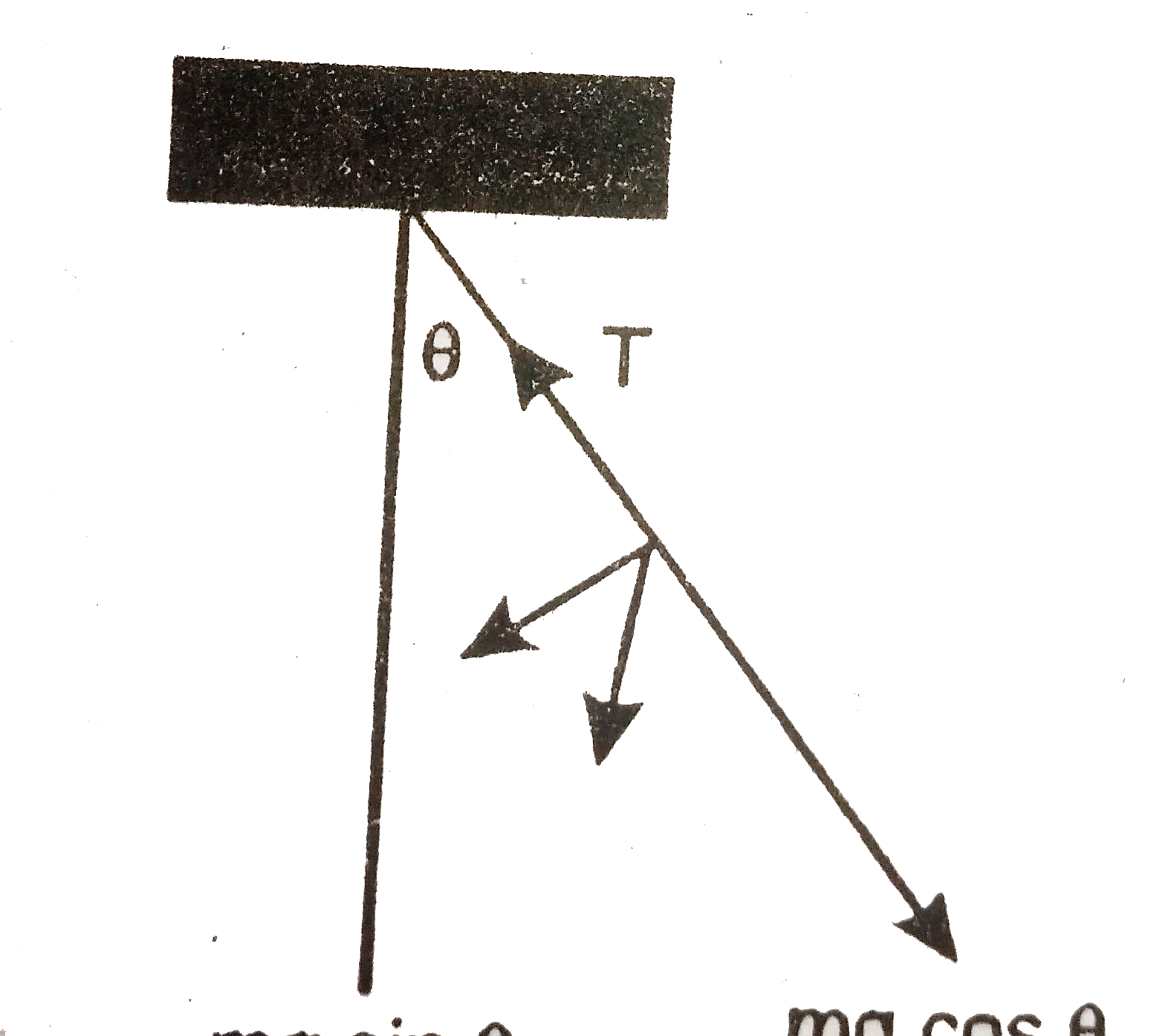Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let theta denote the angular displacement of a simple pendulum oscilla...
Text Solution
|
- Let theta denote the angular displacement of a simple pendulum oscilla...
Text Solution
|
- A simple pendulum of length L and mass (bob) M is oscillating in a pla...
Text Solution
|
- a simple pendulum with a bob of mass m savings with an angular amplitu...
Text Solution
|
- A simple pendulum with charged bob is oscillating with time period T a...
Text Solution
|
- A simple pendulum of Length l and mass (M) is oscillating in a plane a...
Text Solution
|
- A simple pendulum is oscillating with a maximum angular displacement o...
Text Solution
|
- Let theta denote the angular displacement of a simple pendulum oscilla...
Text Solution
|
- the bob of simple pendulum is relasesd when string makes an angle thet...
Text Solution
|