Home
Class 11
PHYSICS
A particle slides on the surface of a fi...

A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.

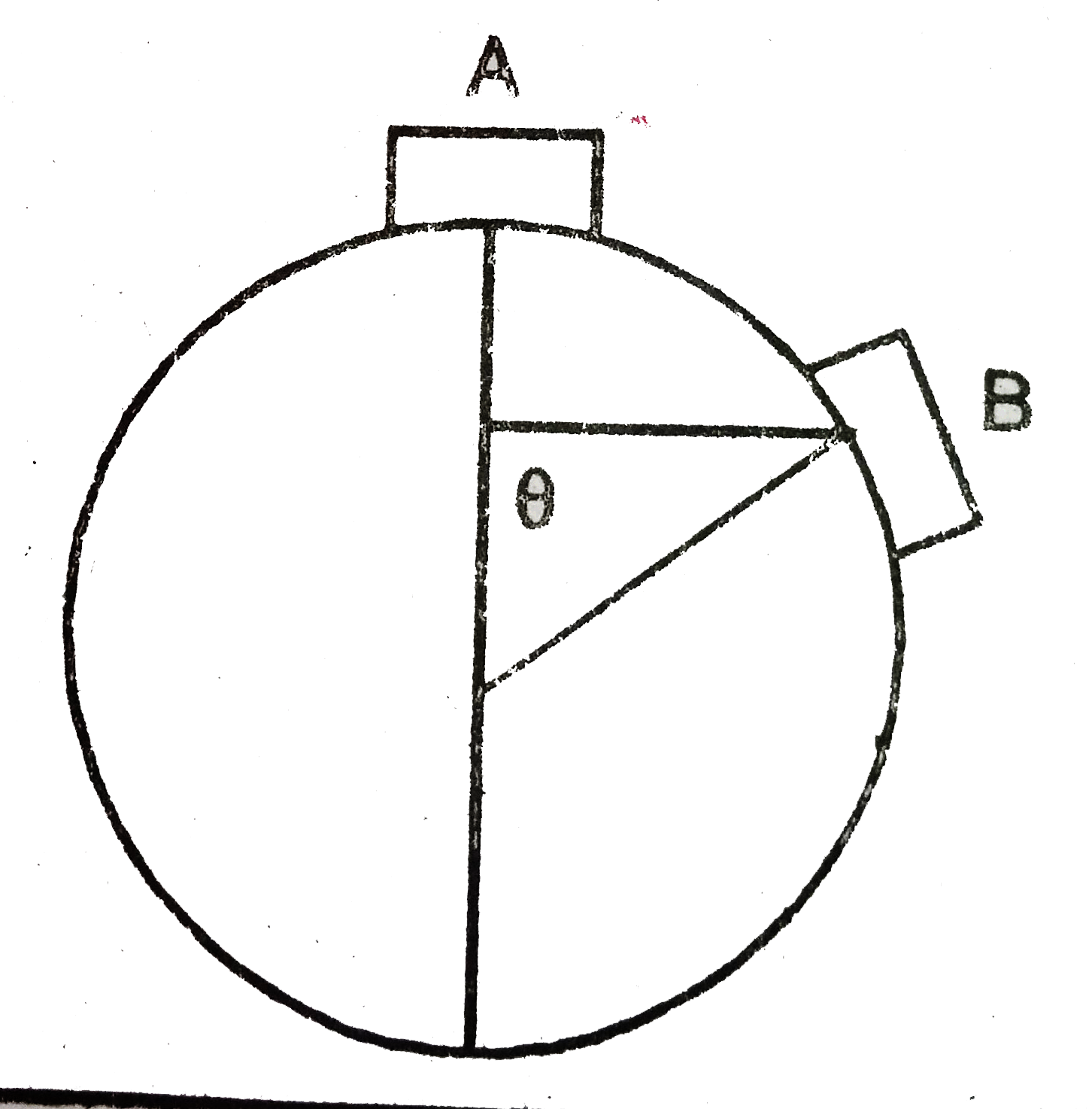
Text Solution

Verified by Experts

The correct Answer is:
A, B, C
Let the velocity be v when the body leaves the surface.
From the free body diagram
`(mv^2)/R=mgcostheta` [because normal reaction]………i
`v^2=Rgcostheta` ……i

Again, from work energy
`principle change in K.E. =work done
`rarr 1/2 mv^2-0=mg(R-Rcostheta)`
`rarr v^2=2gR(1-costheta)` ........ii
From i and ii
`Rgcostheta=2gR(1-costheta)`

`3gRcostheta-2gR`
`costheta=2/3`
`theta=cos^-1(2/3)`
Promotional Banner

Similar Questions

Explore conceptually related problems

A partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :

A particle of mass 10g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between them, to take the particle far away from the sphere (you may take G=6.67xx10^(-11)Nm^(2)//kg^(2))

A particle of mass 10 g is kept of the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle far away from the sphere. (Take G = 6.67 xx 10^(-11) Nm^(2)//kg^(2) ?

A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.

A particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B . At given instant the kinetic energy of the particle is K . Then the force applied by particle on the shell at this instant is :-

A circle is the locus of a point in a plane such that its distance from a fixed point in the plane is constant. Anologously, a sphere is the locus of a point in space such that its distance from a fixed point in space in constant. The fixed point is called the centre and the constant distance is called the radius of the circle/sphere. In anology with the equation of the circle |z-c|=a , the equation of a sphere of radius is |r-c|=a , where c is the position vector of the centre and r is the position vector of any point on the surface of the sphere. In Cartesian system, the equation of the sphere, with centre at (-g, -f, -h) is x^2+y^2+z^2+2gx+2fy+2hz+c=0 and its radius is sqrt(f^2+g^2+h^2-c) . Q. Radius of the sphere, with (2, -3, 4) and (-5, 6, -7) as xtremities of a diameter, is

A hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement theta when velocity of hemisphere has become v is

A bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a dsitance.

A circle is the locus of a point in a plane such that its distance from a fixed point in the plane is constant. Anologously, a sphere is the locus of a point in space such that its distance from a fixed point in space in constant. The fixed point is called the centre and the constant distance is called the radius of the circle/sphere. In anology with the equation of the circle |z-c|=a , the equation of a sphere of radius is |r-c|=a , where c is the position vector of the centre and r is the position vector of any point on the surface of the sphere. In Cartesian system, the equation of the sphere, with centre at (-g, -f, -h) is x^2+y^2+z^2+2gx+2fy+2hz+c=0 and its radius is sqrt(f^2+g^2+h^2-c) . Q. The centre of the sphere (x-4)(x+4)+(y-3)(y+3)+z^2=0 is

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as