Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
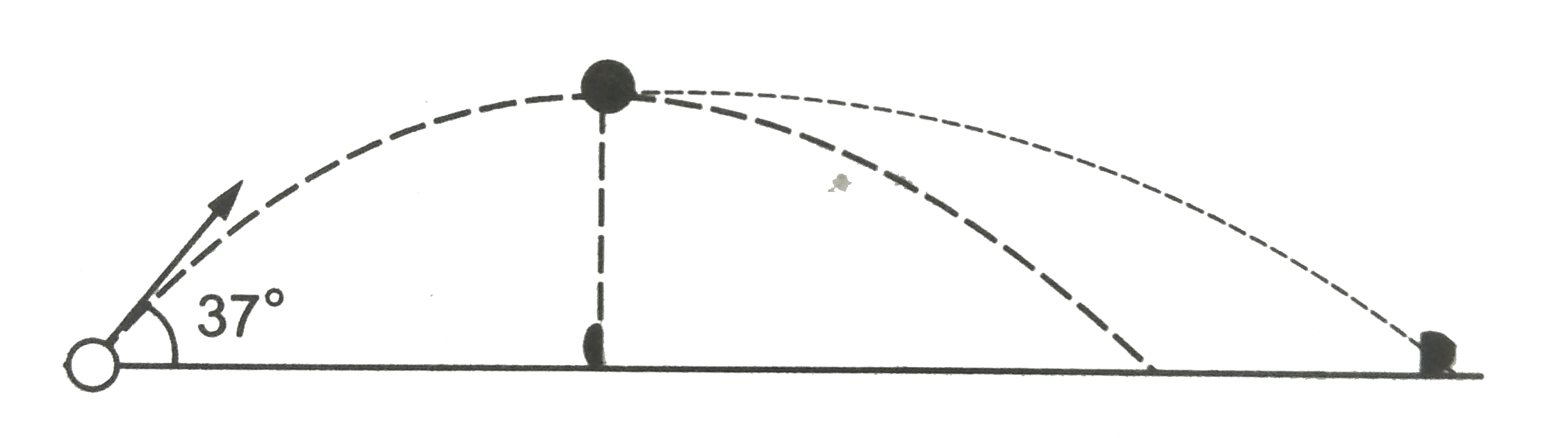
- A projectile is fired at a spedd of 100 m/s at an angel of 37^0 above ...
Text Solution
|
- A projectile is fired at a spedd of 100 m/s at an angel of 37^0 above ...
Text Solution
|
- A bomb of mass 4 m, while moving on a parabolic path, explodes at high...
Text Solution
|
- A projectile of mass 3m explodes at highest point of its path. It brea...
Text Solution
|
- A projectile of mass "m" is projected from ground1 with a speed of 50 ...
Text Solution
|
- A projectile of mass 5m is projected at 40m/s at 75^(@) above horizont...
Text Solution
|
- A body is projected with a speed 160 m/s at an angle 53^(@) with the h...
Text Solution
|
- A projectile of mass M is fired so that the horizontal range is 4 km. ...
Text Solution
|
- A projectile of mass M is fired so that the horizontal range is 4 km. ...
Text Solution
|