Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
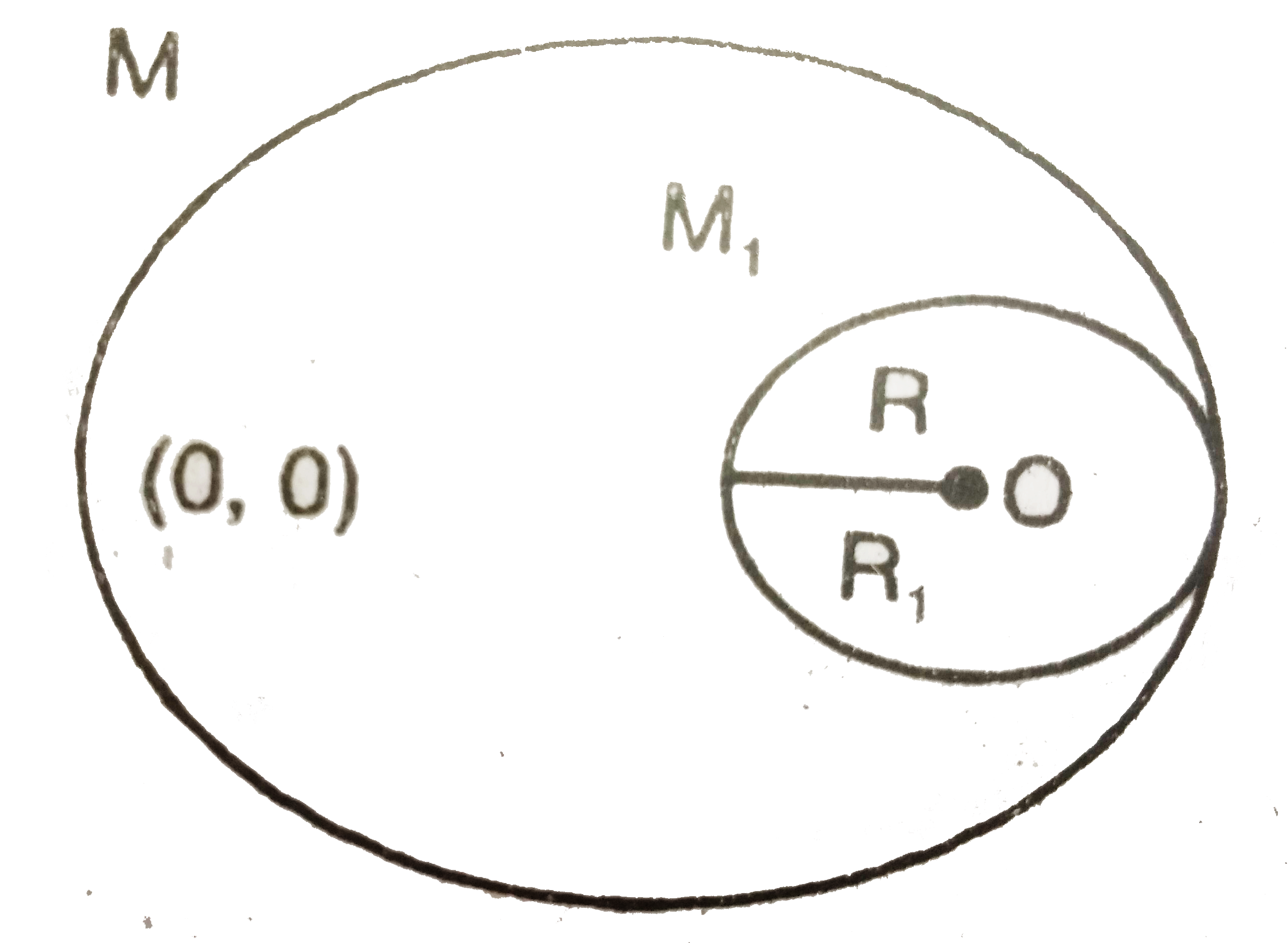
- A uniform disc of radius R is put over another unifrom disc of radius ...
Text Solution
|
- A uniform disc of radius R is put over another unifrom disc of radius ...
Text Solution
|
- A disc of radis R is cut out from a larger disc of radius 2R in such a...
Text Solution
|
- Figure-4.11 shows a circular a disc of radius R from which a small dis...
Text Solution
|
- A circular disc of radius R is removed from a bigger circular disc of ...
Text Solution
|
- A uniform disc of radius R is put over another unifrom disc of radius ...
Text Solution
|
- A uniform disc of radius R is put over another uniform disc of radius ...
Text Solution
|
- A uniform disc of diameter R/2 is put over another uniform disc of dia...
Text Solution
|
- A uniform disc of radius R is put over another uniform disc of radius ...
Text Solution
|