Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
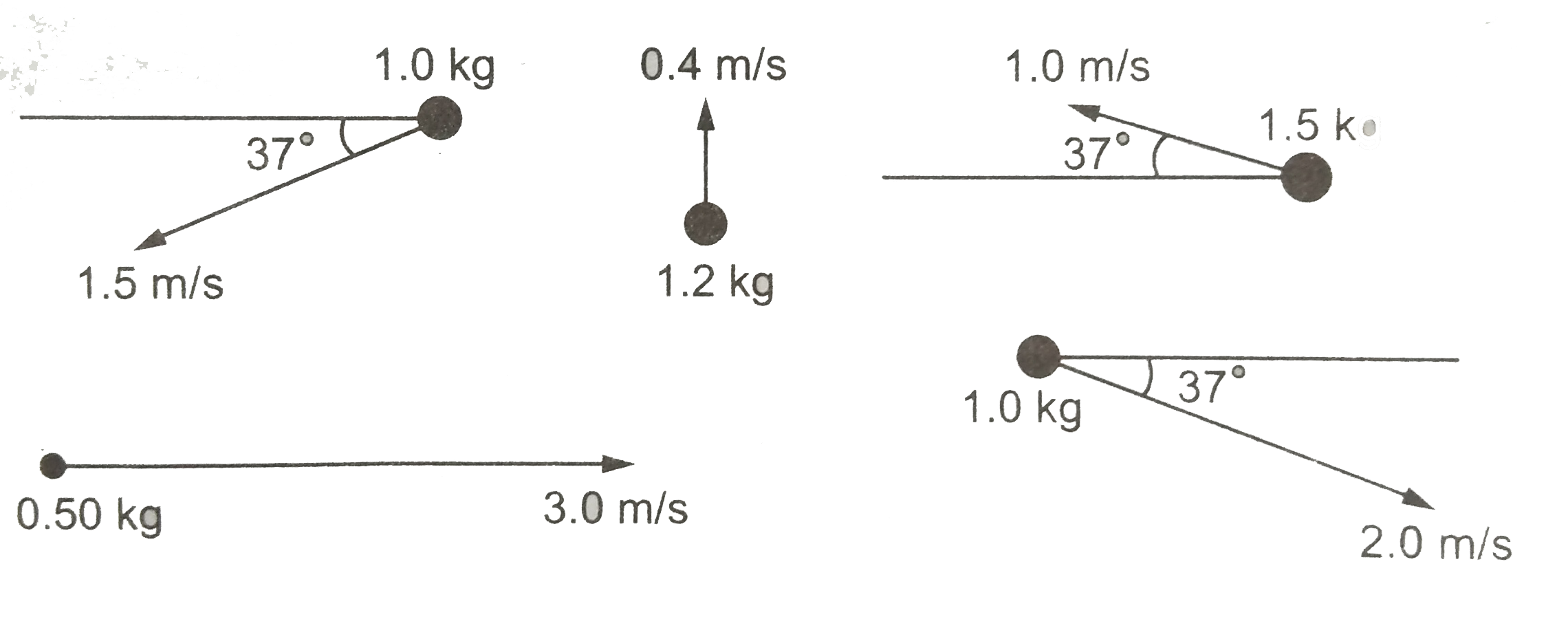
- Calculate the velocity of the centre of mss of the system of particles...
Text Solution
|
- Calculate the velocity of the centre of mss of the system of particles...
Text Solution
|
- The velcoity of centre of mass of the system as shown in the figure :-
Text Solution
|
- The velocity (in m/s) of centre of mass of the system as shown in the ...
Text Solution
|
- The velocity of the centre of mas of the system of two particle each o...
Text Solution
|
- The coordinate of the centre of mass of a system as shown in figure : ...
Text Solution
|
- The coordinate of the centre of mass of a system as shown in figure : ...
Text Solution
|
- The acceleration of centre of mass of system as shown in figure is
Text Solution
|
- Calculate the velocity of the centre of mss of the system of particles...
Text Solution
|