Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
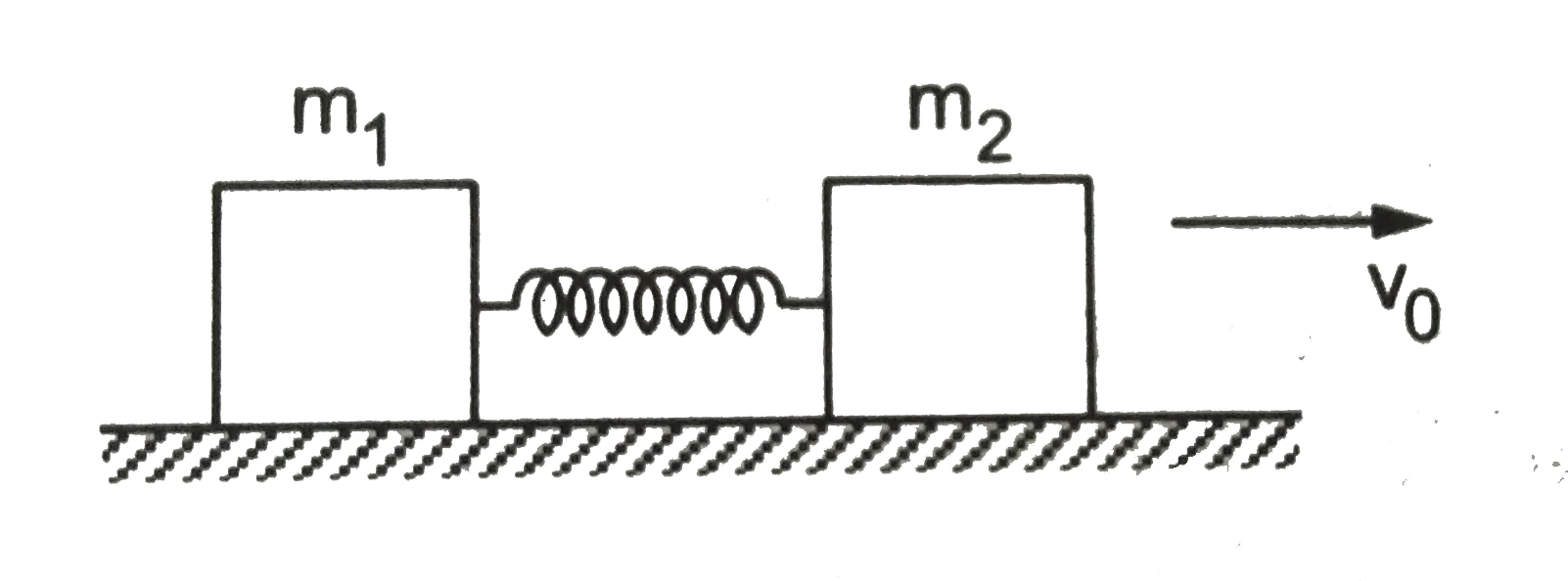
- Two blocks of masses m1 and m2 are connected by a spring of spring con...
Text Solution
|
- Two blocks of masses m1 and m2 are connected by a spring of spring con...
Text Solution
|
- A spring-mass system ( m1 + massless spring + m2 ) fall freely from a ...
Text Solution
|
- A block of mass m moving at a speed v0 compresses a spring of spring c...
Text Solution
|
- Two blocks of masses m1 and m2 are attached to the lower end of a ligh...
Text Solution
|
- Block of mass 2 m is given v(0) towards the right. If L is the natural...
Text Solution
|
- A block of mass m1 is lying on the edge of a rough table. The coeffici...
Text Solution
|
- Blocks A&B of mass m each are connected with spring of constant k both...
Text Solution
|
- The block of mass m is released when the spring was in its natrual len...
Text Solution
|