Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
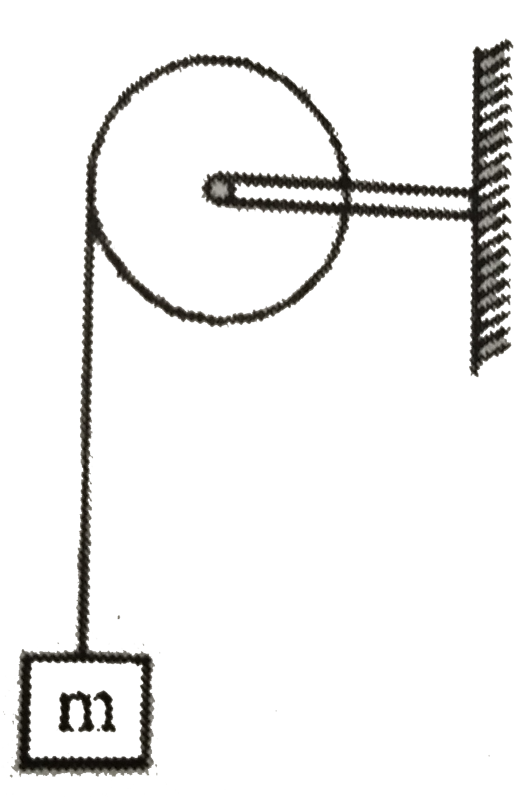
- A disc of mass m and radius r is free to rotate about its centre as sh...
Text Solution
|
- A wheel of moment of inertia I and rdius r is free to rotate about its...
Text Solution
|
- A mass less string is wrapped around a uniform disc of mass m and radi...
Text Solution
|
- A disc of mass m and radius r is free to rotate about its centre as sh...
Text Solution
|
- A uniform disc of radius R and mass M is free to rotate only about its...
Text Solution
|
- A disc of mass M has a light, thin string wrapped several times around...
Text Solution
|
- A block of mass m is attached to one end of a light string which is wr...
Text Solution
|
- A uniform disc of mass M and radius R is mounted on a fixed horizontal...
Text Solution
|
- A uniform disc of radius R and mass M is free to rotate about a fixed ...
Text Solution
|