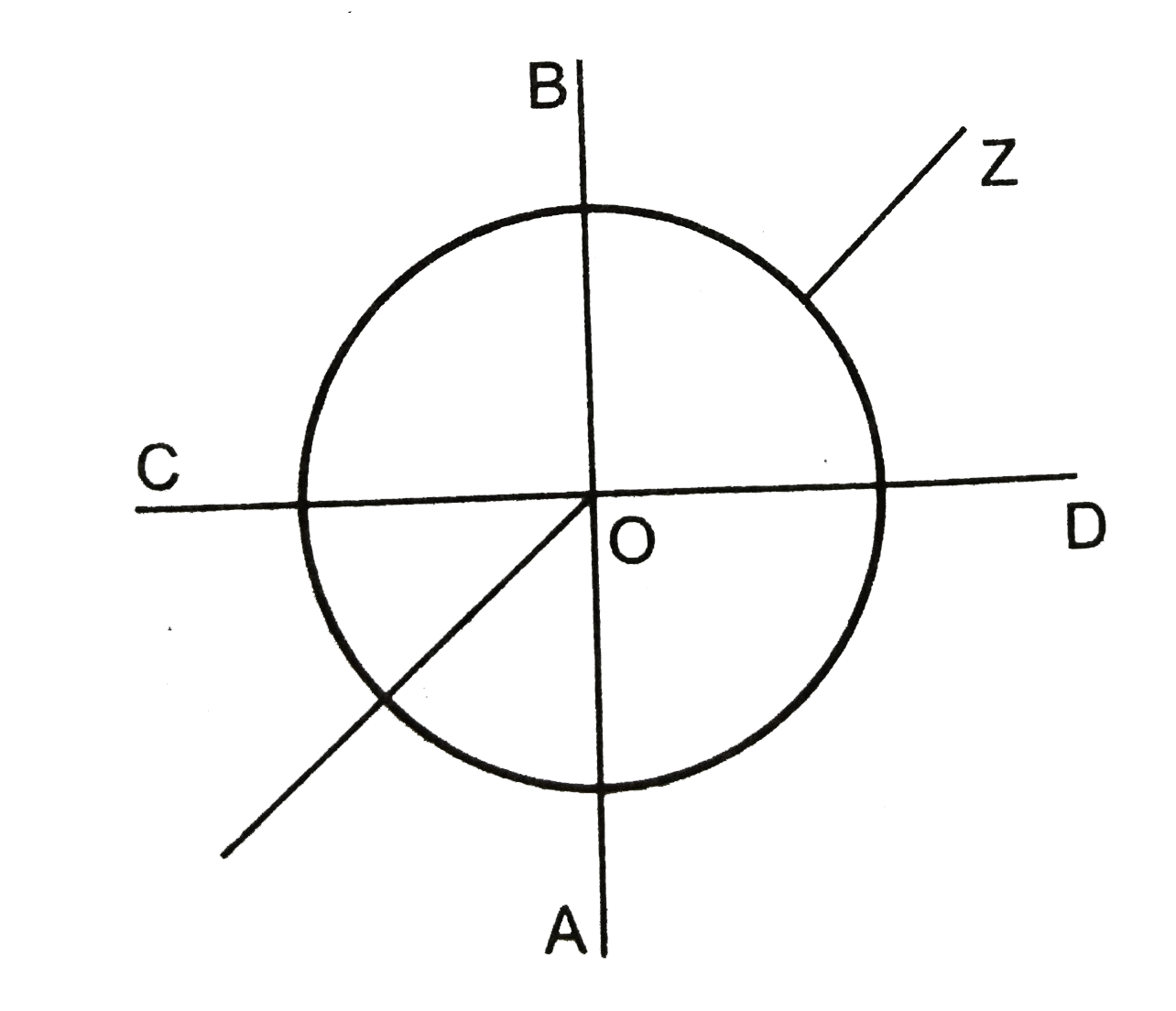
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the moment of inertia of a uniform ring of mass M and radius R ab...
Text Solution
|
- Find the moment of inertia of a uniform rign of mass M and radius R ab...
Text Solution
|
- Calculate the moment of inertia of a. a ring of mass M and radius R ab...
Text Solution
|
- Moment of inertia of a uniform circular ring of mass 2 kg and diameter...
Text Solution
|
- Moment of inertia of a uniform circular ring of mass M and radius R ab...
Text Solution
|
- Find the moment of inertia of uniform ring of mass M and radius R abou...
Text Solution
|
- The moment of inertia of a ring of mass M and radius R about PQ axis w...
Text Solution
|
- The moment of inertia of a ring of mass M and radius R about PQ axis w...
Text Solution
|
- Find the moment of inertia, about a diameter, of a uniform ring of mas...
Text Solution
|