Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
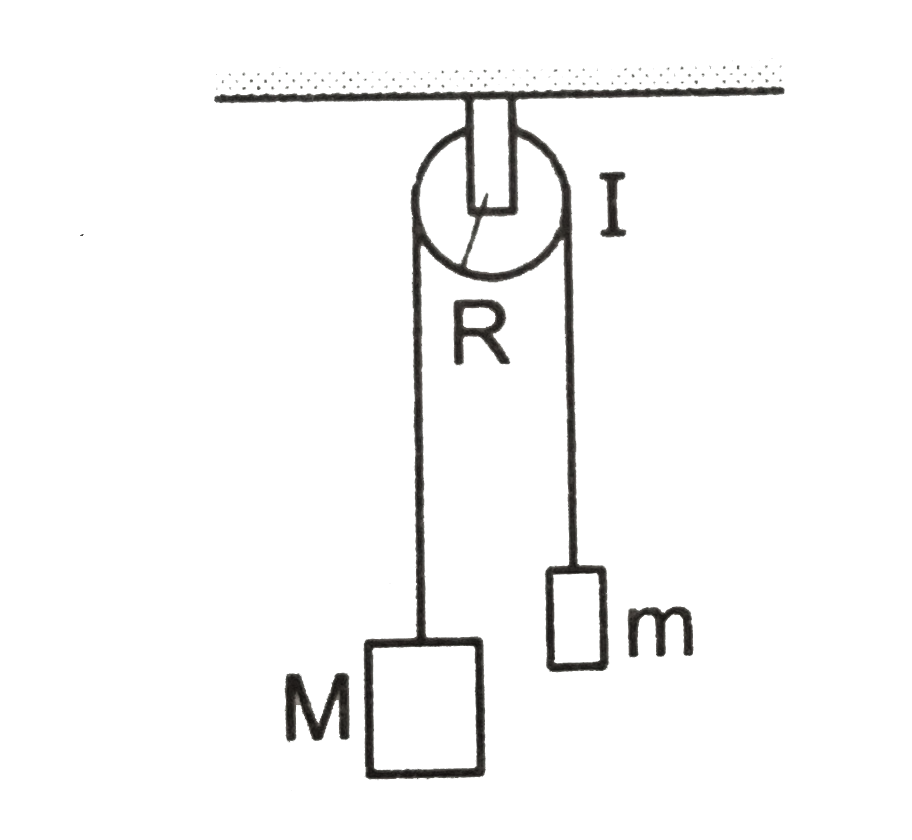
- The pulley shown in figure has a moment of inertia I about it's axis a...
Text Solution
|
- Consider the situation shown in figure. All the surfaces are frictions...
Text Solution
|
- The pulley shown in figure has a moment of inertia I about it's axis a...
Text Solution
|
- Solve the previous problem if the pulley has a moment of inertia I abo...
Text Solution
|
- Consider the situation as shown. The pulley has a moment of inertia I,...
Text Solution
|
- An object of mass m is tied to a light string wound around a pulley th...
Text Solution
|
- Two blocks are connected by a string that passes over a pulley of radi...
Text Solution
|
- चित्र 18.W3 में दिखाई गई घिरनी की त्रिज्या R तथा अपने अक्ष के प्रति जड...
Text Solution
|
- दो द्रव्यमान तथा M एक घिरनी पर से होकर गुजर रही एक रस्सी से जुड़ हुए ह...
Text Solution
|