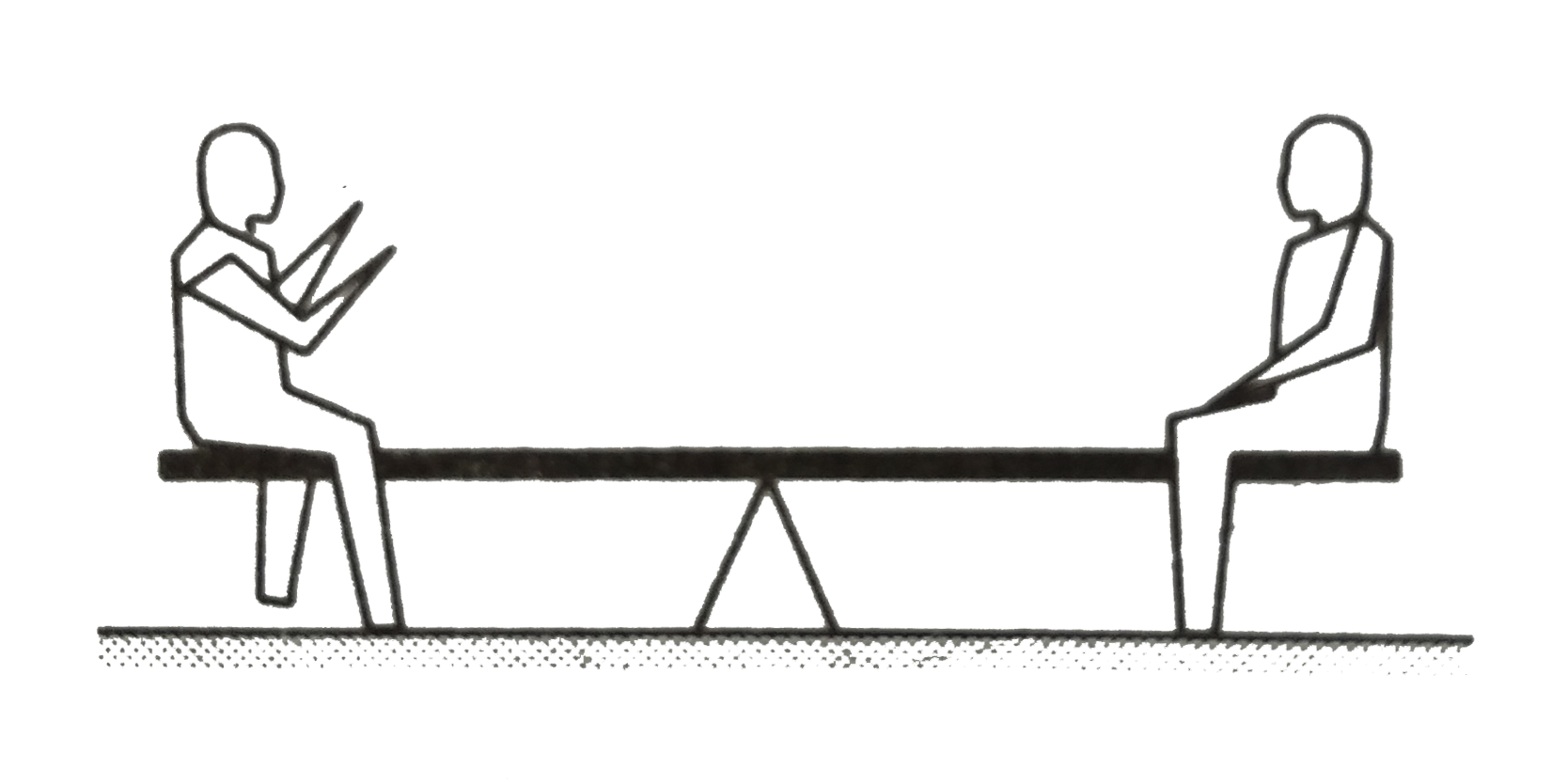
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two small kids weighing 10 kg and 15 kg respectively are tyribg t bal...
Text Solution
|
- In a children's park a heavy rod is pivoted at the centre and is made ...
Text Solution
|
- Two small kids weighing 10 g and 15 kg respectively are tyribg t balan...
Text Solution
|
- A 20 kg kid is sitting in a 60 kg boat in a lake. The distance of kid ...
Text Solution
|
- 4 मीटर लम्बाई के एक सी-सा का आलम्ब मध्य में इसके एक सिरे पर 15 किग्रा ...
Text Solution
|
- 6 m long see-saw remains horizontal when two children weighing 20 kg a...
Text Solution
|
- A see-saw of length 6m is pivoted at its centre. A child (A) of mass 2...
Text Solution
|
- Two children weighing 15 kg, wt and 25 kgwt. sit at the ends of a see-...
Text Solution
|
- Two boys weighing 30kg and 50kg are sitting on either side of the fulc...
Text Solution
|