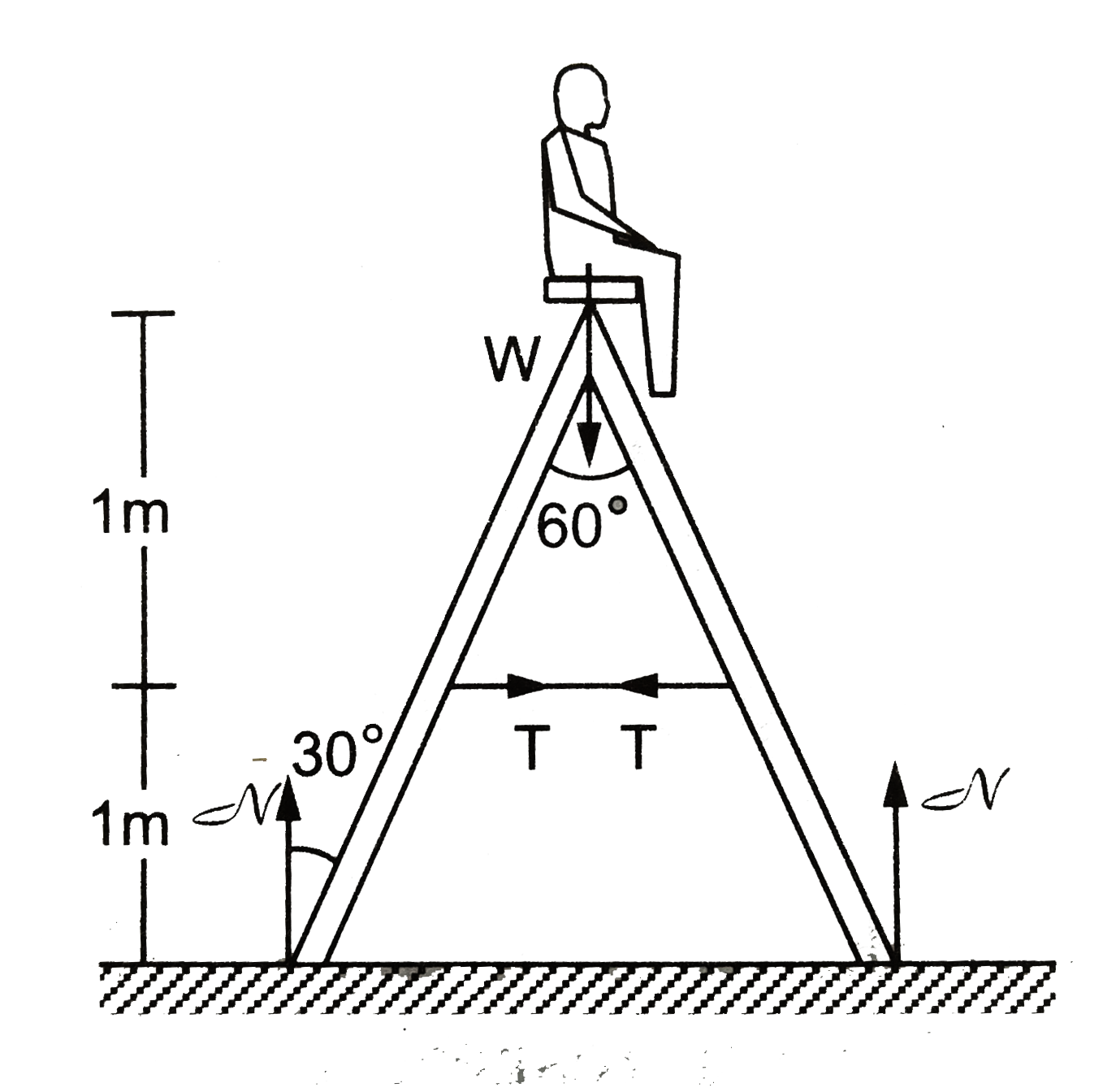Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ladder shown in figure has negligible mass and rests on a friction...
Text Solution
|
- A uniform ladder of mass 10 kg leans against a smooth vertical wall ma...
Text Solution
|
- The ladder shown in figure has negligible mass and rests on a friction...
Text Solution
|
- In the figure, a ladder of mass m is shown leaning against a wall. It ...
Text Solution
|
- A ladder rests on the floor of a room, leaning agains a wall. If the c...
Text Solution
|
- सलग्न चित्र में दिखाया गया है की एक खड़ी होने वाली सीढ़ी के दो पक्षों BA...
Text Solution
|
- चित्र 18.W6 जो एक चिकनी क्षैतिज सतह पर रख है। सीईी के दो हिस्से 60^@ क...
Text Solution
|
- जैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और...
Text Solution
|
- A uniform ladder is standing against a vertical smooth wall, resting o...
Text Solution
|