Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
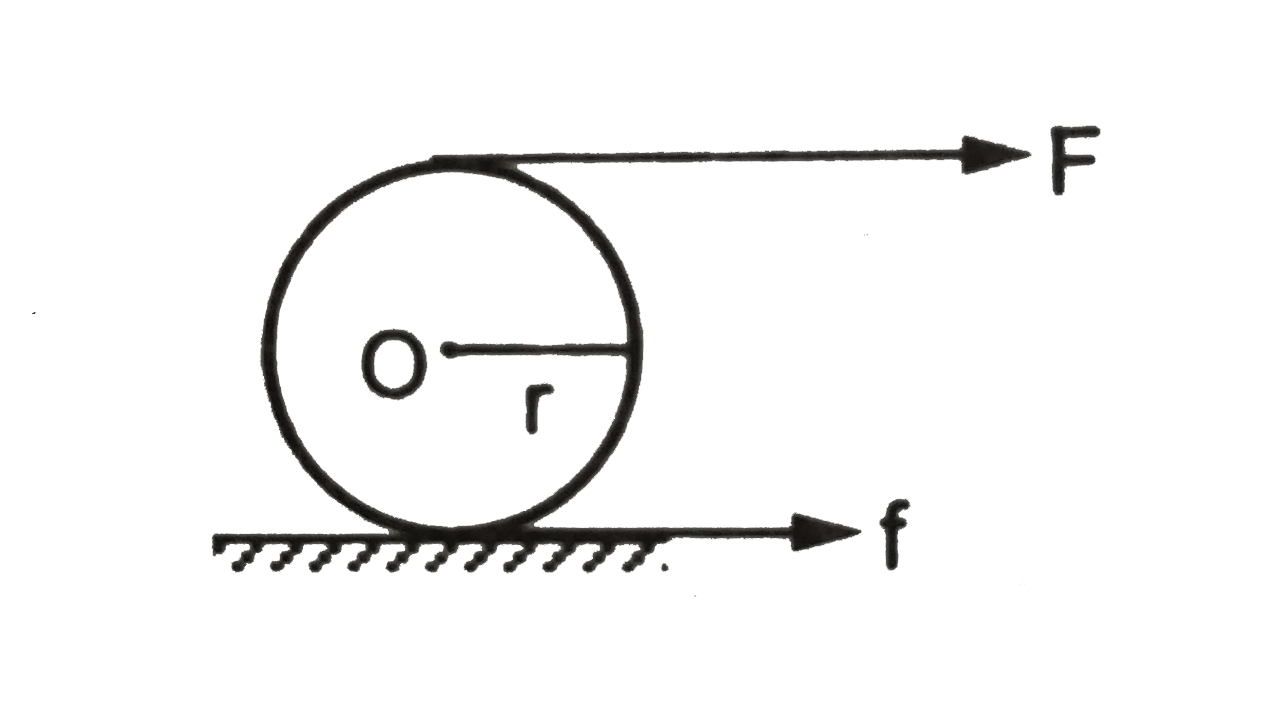
- A force F acts tangentially at the highest point of a sphere of mass m...
Text Solution
|
- A force F acts tangentially at the highest point of a sphere of mass m...
Text Solution
|
- A force F acts tangentially at the highest point of a sphere f mass m ...
Text Solution
|
- A force F acts tangentially at the highest point of a disc of mass m k...
Text Solution
|
- A sphere of mass M rolls without slipping on rough surface with centre...
Text Solution
|
- A force F acts tangentially at the highest point of a solid cylinder o...
Text Solution
|
- A solid sphere of mass ma nd radis R is placed on a rough horizontal s...
Text Solution
|
- A solid sphere of radius R is rolled by a force F acting at the topo o...
Text Solution
|
- A solid sphere of mass 2kg is pulled by a constant force acting at its...
Text Solution
|