Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then
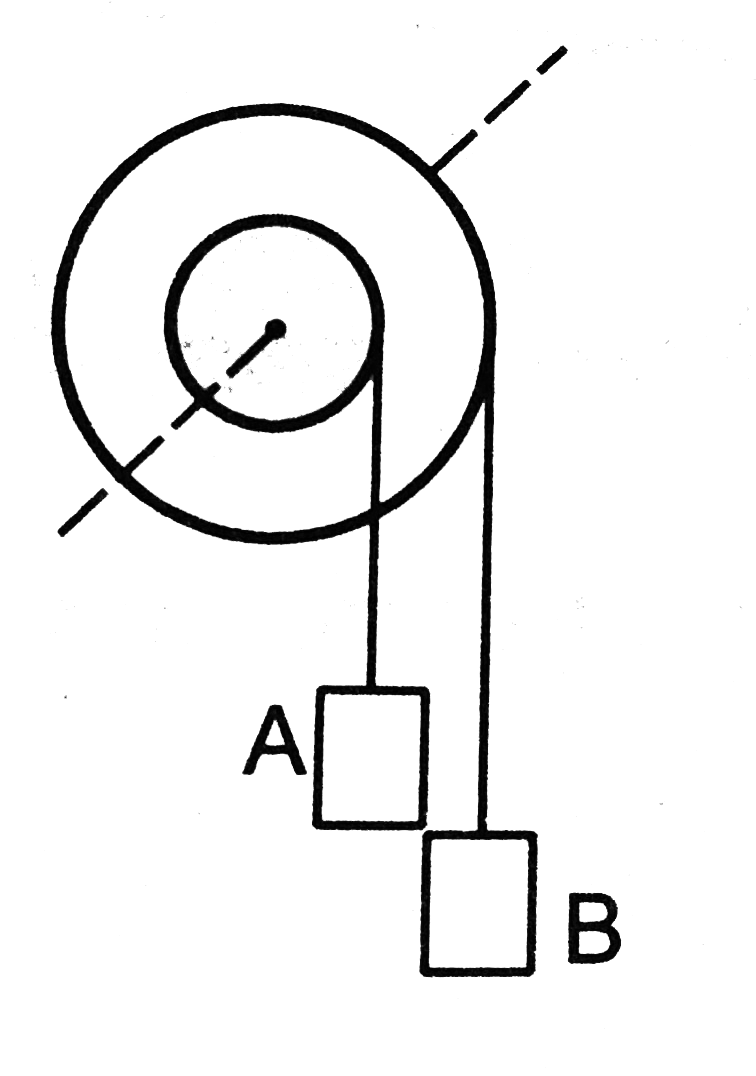
Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then


A
`x=2y`
B
`x=y`
C
`y=2x`
D
none of these
Text Solution
Verified by Experts
The correct Answer is:
C
Similar Questions
Explore conceptually related problems
A bob of mass m is attached at one end of a string of length l other end of the string is fixed at point O . Bob is rotating in a circular path of radius l in horizontal plane about O with constant speed v , as shown in the figure. The average force exterted by string on the bob during its :- (A) half revolution will be (mv^(2))/(pil) (B) half revolution will be (2mv^(2))/(pil) (C) one fourth revolution will be (sqrt2mv^(2))/(pil) (D) one revolution will be zero Select correct alternative :-
A uniform disc of mass M =2.50 kg and radius R = 0.20 m is mounted on an axle supported on fixed frictionless bearings. A light cord wrapped around the rim is pulled with a force 5 N. On the same system of pulley and string, instead of pulling it down, a body of weight 5 N is suspended. If the first processis termed A and the second B, the tangential acceleration of point P will be:
Figure shows a pulley block system in which a block A is hanging one side of pulley and an other side a small bead B of mass m is welded on pe=ulley. The moment of intertia of pulley is I and the sytem is in equilibrium position when bead is at an angle alpha from the vertical. If the system is slightly disturbed from its equlibrium position, find the time period of its oscillations.
(a) Magnetic field lines show the direction (at every point) along which a small magnetised needle aligns at the point). Do the magnetic field lines also represent the lines of force on a moving charged particle at every point? (b) Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why? (c) If magnetic monopoles existed, how would the Gauss's law of magnetism be modified? (d) Does a bar magnet exert a torque on itsell due to its own field? Does one element of a current-carrying wire exert a force on another element of the same wtre? (e) Magnetic field arises due to charges in motion. Can a system have magnetic moments even though its net charge is zero?
A wheel having n conducting concentric spokes is rotating about it geometrical axis with an angular velocity omega , in a uniform magnetic field B perpendicular to its plane prove that the induced emf generated between the rim of the wheel and the center is (omegaBR^2)/2 , where R is the radius of the wheel. It is given that the rim of the wheel is conducting.
A line charge lambda per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light nonconducting spokes and is free to rotate without friction about its axis as per figure. A uniform magnetic field extends over a circular region within the rim. It is given by, B=-B_0 k ( r le a , a lt R) =0 (otherwise) What is the angular velocity of the wheel after the field is suddenly switched off ?
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity omega is an example of non=inertial frame of reference. The relationship between the force vecF_(rot) experienced by a particle of mass m moving on the rotating disc and the force vecF_(in) experienced by the particle in an inertial frame of reference is vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega . where vecv_(rot) is the velocity of the particle in the rotating frame of reference and vecr is the position vector of the particle with respect to the centre of the disc. Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed omega about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (vecomega=omegahatk) . A small block of mass m is gently placed in the slot at vecr(R//2)hati at t=0 and is constrained to move only along the slot. The distance r of the block at time is
Consider two satellites A and B of equal mass m, moving in the same circular orbit of radius r around the earth E but in opposite sense of rotation and therefore on a collision course (see figure) (i). In terms of G,M_(e) m and r find the total mechanical energy E_(A)+E_(B) of the two satellite plus earth system before collision (ii). If the collision is completely inelastic so that wreckage remains as one piece of tangled material (mass=2m) find the total mechanical energy immediately after collision. (iii). Describe the subsequent motion of the wreckage.
Recommended Questions
- Figure shows a small wheel fixed coaxially on a bigger one of double t...
Text Solution
|
- Figure shows a small wheel fixed coaxially on a bigger one of double t...
Text Solution
|
- Two wheels A and C are connected by a belt B as shown in figure. The r...
Text Solution
|
- A wheel A is connected to a second wheel B by means of inextensible st...
Text Solution
|
- Wheels A and B in Figure are connected by a belt that does not slip. T...
Text Solution
|
- A wheel of radius R rolls without slipping on a horizontal ground. The...
Text Solution
|
- A wheel is made to roll without slipping, towards right, by pulling a ...
Text Solution
|
- A wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt...
Text Solution
|
- चित्र में A और B दो पहिये हैं, जो एक ही बेल्ट द्वारा जुड़े हुए हैं । B ...
Text Solution
|