Home
Class 11
PHYSICS
When a force of 6.0 N is exerted at 30^@...

When a force of 6.0 N is exerted at `30^@` to a wrench at a distance of 8 cm from the nut, ilt is just able to losen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

Text Solution

Verified by Experts

The correct Answer is:
A
A force 6 N acting at angle of `30^@` is just able to loosen the wrench at a distance 8 cm from it.
therefore total torque acting at A about the point O.

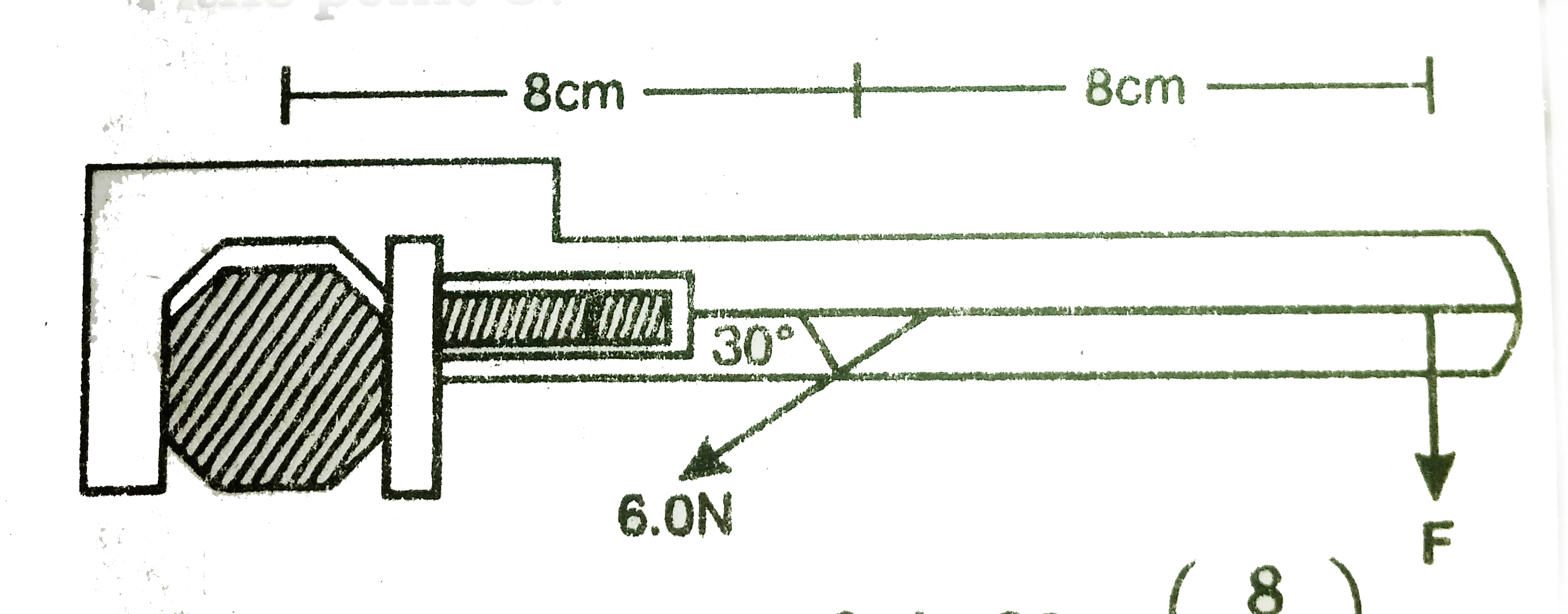
=6sin30^@xx(8/100)`
threfore total torque required at b about the point O.
`=Fxx16/100`
`rarr Fxx16/100=6sin30^@xx8/100
`rarr F=(8xx3)/16=1.5N`
Promotional Banner

Similar Questions

Explore conceptually related problems

A very long straight wire carries a current of 5 A. An electron moves with a velocity of 10^(6)ms^(-1) remaining parallel to the wire at a distance of 10 cm from wire in a direction opposite to that of electric current. Find the force on this electron. (Here the mass of electron is taken as constant) (e=-1.6xx10^(-19)C,mu_(0)=4pixx10^(-7)SI)

A block of mass 0.9 kg attached to a spring of force constant k is lying on a frictionless floor. The spring is compressed to sqrt(2) cm and the block is at a distance 1//sqrt(2) cm from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is 0.2 sec . Find the approximate value of k

Three parallel forces are acting on a rod at distances of 40 cm, 60 cm and 80 cm respectively from one end of the rod (as shown in figure). Assuming no other forces, the rod under the influence of these forces will :-

A particle of mass 0.3 kg subject to a force F=-kx with k=15N//m . What will be its initial acceleration if it is released from a point 20cm away from the origin?

A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity vecV_0 = vacV_0hati. The coefficinet of friction is mu. The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.

A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, (a) the wire intersects the axis, (b) the wire is turned from N-S to northeast-northwest direction, (c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?

An electric dipole is prepared by taking two electric charges of 2 xx 10^(-8) C separated by distance 2 mm. This dipole is kept near a line charge distribution having density 4 xx 10^(-4) C/m in such a way that the negative electric charge of the dipole is at a distance 2 cm from the wire as shown in the figure. Calculate the force acting on the dipole. [Take k=1/(4piepsilon_(0)) = 9 xx 10^(9) Nm^(2)C^(-2) ]

A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v_(0) at a trajectory that makes an angle theta=45^(@) with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10, 000N over a very short time of 0.24s . The height above the ground at which the clown begins his trajectory is 10m . A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses. From figure 2, approximately how much time will it take for clown with a mass of 60 kg to reach the safety net located 10 m below the height of the cannot?

A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v_(0) at a trajectory that makes an angle theta=45^(@) with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10, 000N over a very short time of 0.24s . The height above the ground at which the clown begins his trajectory is 10m . A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses. If the angle the cannot makes with the horiaontal is increased from 45^(@) , the hoop will have to be

A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v_(0) at a trajectory that makes an angle theta=45^(@) with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10, 000N over a very short time of 0.24s . The height above the ground at which the clown begins his trajectory is 10m . A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses. If the clown's mass is 80 kg , what initial velocity v_(0) will have as he leaves the cannot?