Home
Class 11
PHYSICS
Find the order of the differential equat...

Find the order of the differential equation ` 9((d^2y)/dx^2)−7(dy/dx)+y^6=0`
a) 3
b) 1
c) 6
d) 2

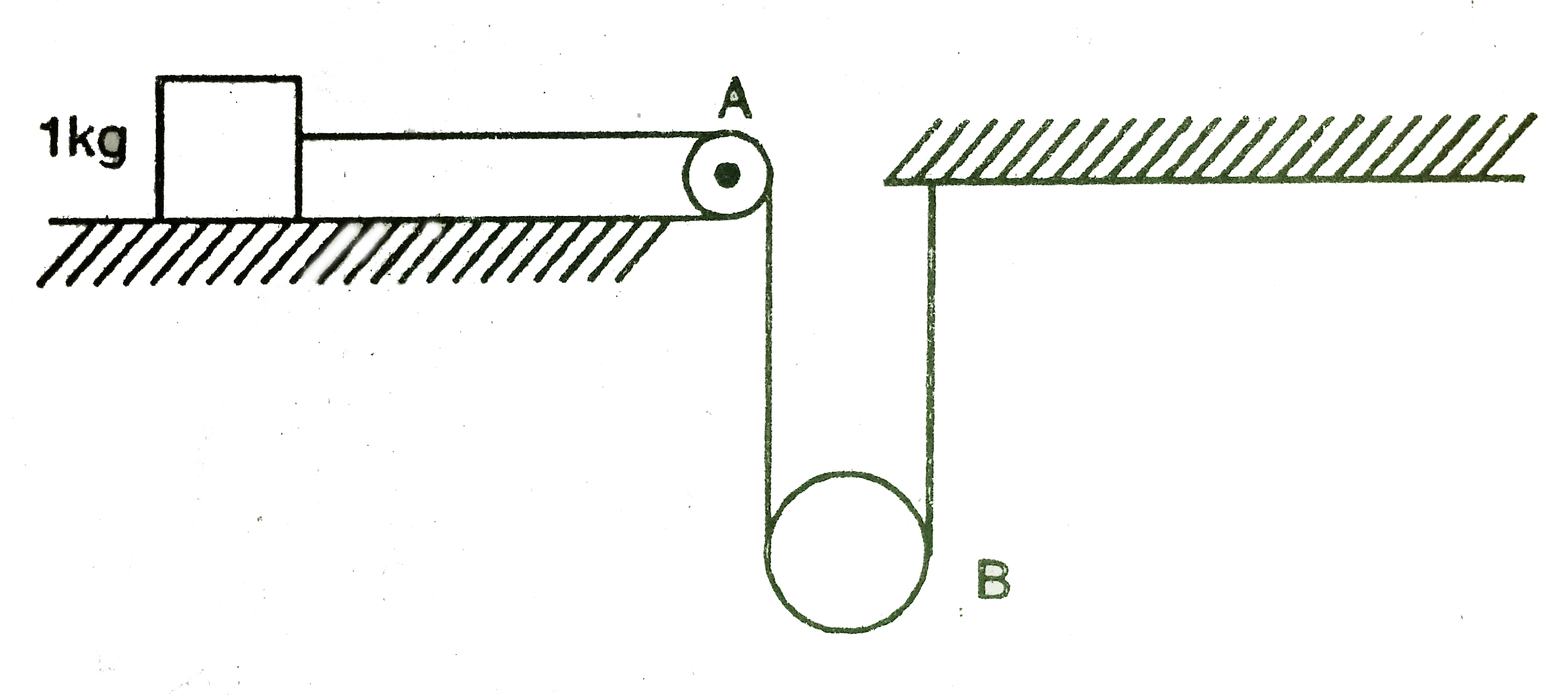
Text Solution

Verified by Experts

The correct Answer is:
A, B
A is light pulley and B is the descending puley having I=0.20 kg-m^2 and r=0.2 m
Mass of the block =1kg
According to the question
`T_1=m_1a`……….1
`(T_2-T_1)r=Ialpha`……2
`m_2g=m_2alpha a/2=T_1+T_2`……. 3
`T_2-T_1=(Ia)/(2r^2)=(5a)/2`
and `T_1=a` (because `alpha=a/(2r))`
`rarr T_2=/2a`

`rarr m_2g=m_2a/2+7/5a+a`
[using 3]
`rarr (2I)/r^2g=(2I)/r^2a/2+9/2as (1/2mr^2=I)`
`rarr 98.5a+4.5a`
`rarr a=98/9.5=10.3 m/s^2`
Promotional Banner

Similar Questions

Explore conceptually related problems

The order of the differential equation 2x^(2) (d^(2)y)/(dx^(2))-3(dy)/(dx) + y = 0 is

The differential equation x(dy)/(dx)+(3)/((dy)/(dx))=y^(2)

Solve the differential equation (dy)/(dx)=(x+2y-1)/(x+2y+1).

Solve the differential equation (dy)/(dx)=(2y-6x-4)/(y-3x+3).

Find the general solution of the differential equation x (dy)/(dx) + 2y = x^(2)(x ne 0) .

Verify that the function y = c_(1) e^(ax) cos bx + c_(2)e^(ax) sin bx , where c_(1),c_(2) are arbitrary constants is a solution of the differential equation (d^(2)y)/(dx^(2)) - 2a(dy)/(dx) + (a^(2) + b^(2))y = 0

Integrating factor of the differential equation y dx - ( x-2y^(2) ) dy=0 is …..

The degree of the differential equation (d^(2)y)/(dx^(2))^(3) + ((dy)/(dx))^(2) + sin ((dy)/(dx)) + 1 = 0 is