Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
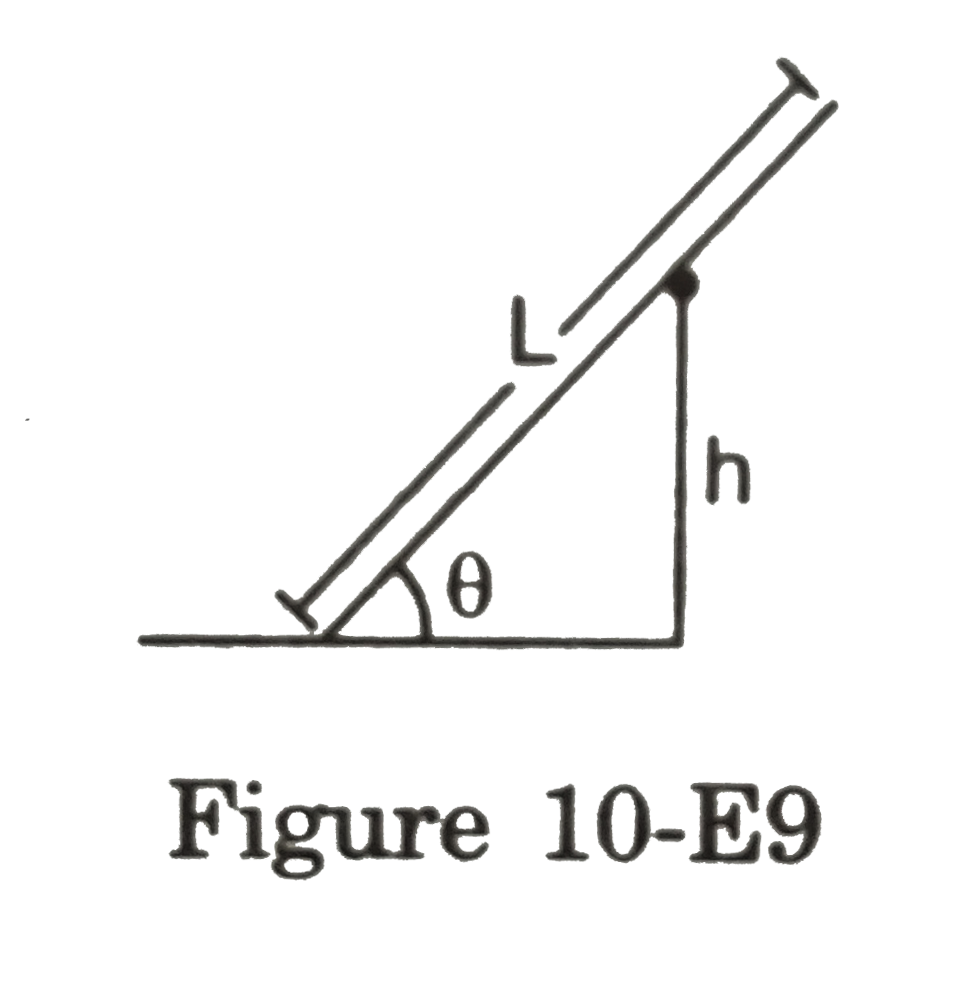
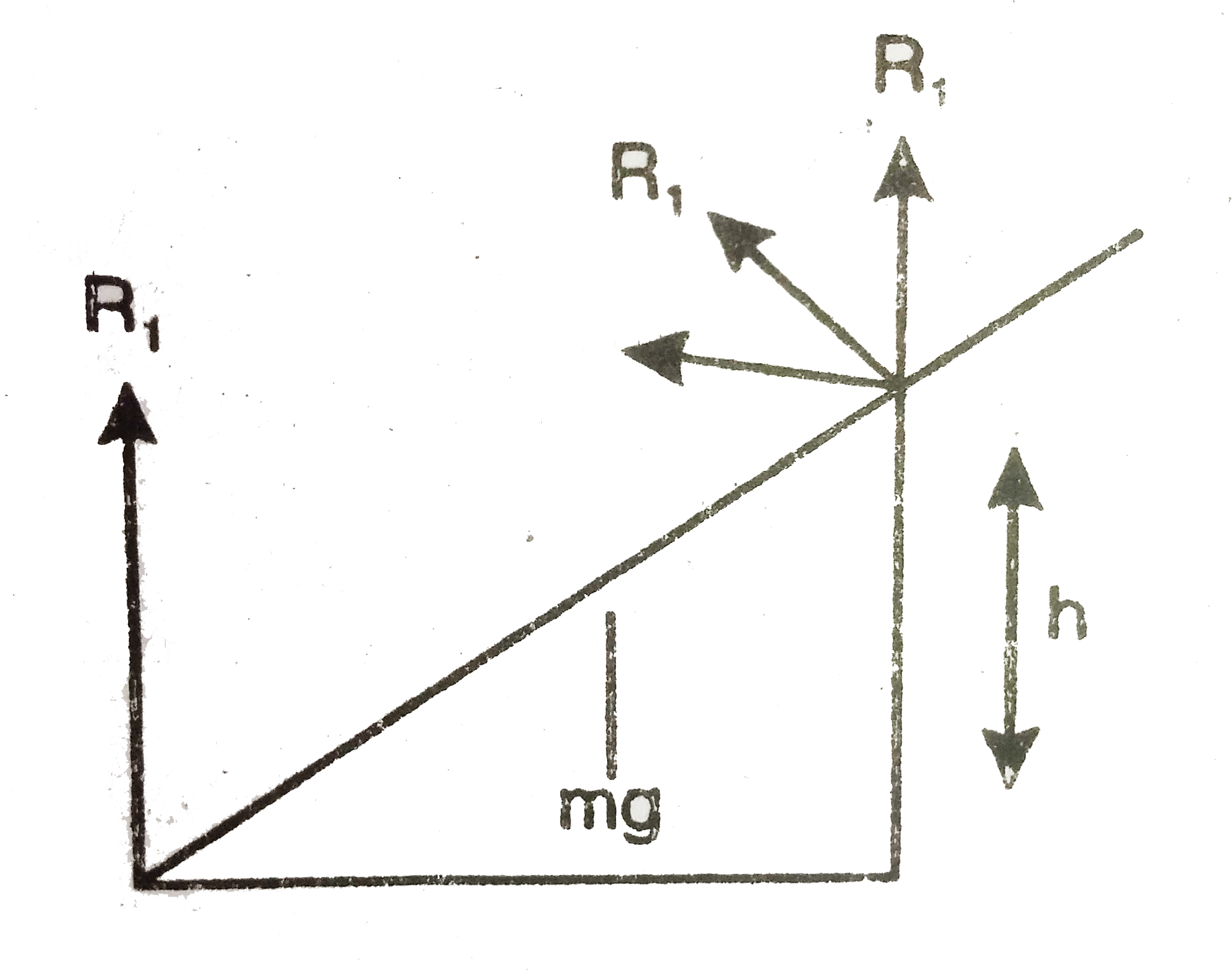
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- A uniform thin rod of mass m and length l is standing on a smooth hori...
Text Solution
|
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- A uniform ladder of length l rests against a smooth, vertical wall (fi...
Text Solution
|
- A rod of length 'l' is inclined at an angle 'theta' with the floor aga...
Text Solution
|
- Consider a rod of length l resting on a wall and the floor. If the vel...
Text Solution
|
- L लंबाई की एक समरूप छड़ एक चिकने रोलर पर चित्र 18.E8 में दिखाए अनुसार ...
Text Solution
|
- A stationary uniform rod of mass 'm', length 'l' leans against a smoo...
Text Solution
|