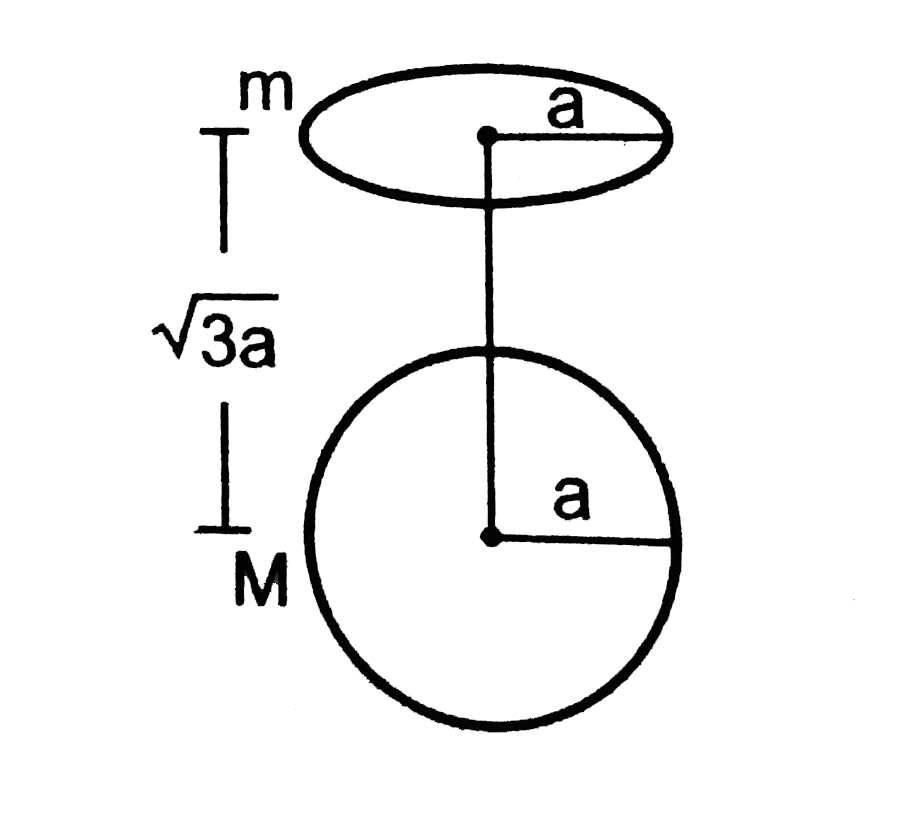Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform rig of mas m and radius a is placed directly above a uniform...
Text Solution
|
- A uniform rig of mas m and radius a is placed directly above a uniform...
Text Solution
|
- A uniform ring of mass m is lying at a distance sqrt(3) a from the cen...
Text Solution
|
- Find the centre of mass of a uniform semicircular ring of radius R and...
Text Solution
|
- A uniform sphere has a mass M and radius R. Find the pressure p inside...
Text Solution
|
- A uniform ring of mass M and radius R is placed directly above a unifo...
Text Solution
|
- A uiform ring of mass M and radius R is placed directly above a unifor...
Text Solution
|
- A uniform ring of mass m and radius 3a is kept above a sphere of mass ...
Text Solution
|
- द्रव्यमान m एवं त्रिज्या a का एक समरूप वलय M द्रव्यमान के एक...
Text Solution
|