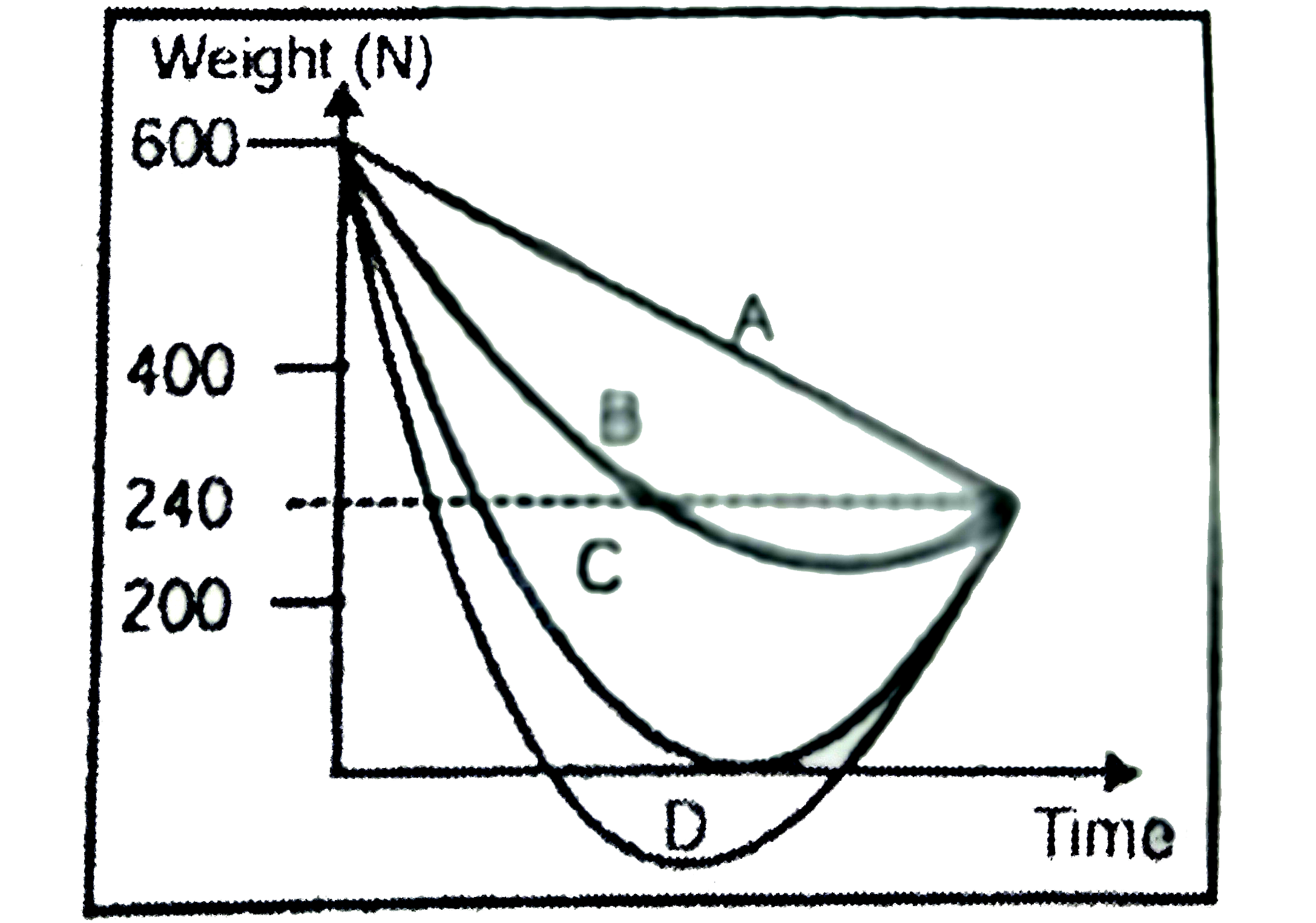
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Suppose the acceleration due to gravity at the earth's surface is 10 m...
Text Solution
|
- Suppose the acceleratio due to gravity at thth's surface is 10ms^-2 an...
Text Solution
|
- The radius of earth is about 6400Km and that of mars is about 3200 km ...
Text Solution
|
- The acceleration due to gravity on the surface of the earth is 10 ms^(...
Text Solution
|
- The radius of Mars is 3.4 xx 10^(6)m and the accelerationof a freely f...
Text Solution
|
- मान ले कि पृथ्वी की सतह पर गुरूत्वीय त्वरण 10 m//s^(2) है तथा मं...
Text Solution
|
- Assuming the mass of Earth to be ten times the mass of Mars, its radiu...
Text Solution
|
- माना कि पृथ्वी की सतह पर गुरूत्वीय त्वरण 10 m/स^२ है मंगल की सतह पर 4....
Text Solution
|
- Suppose the acceleration due to gravity at earth's surface is 10ms^-2 ...
Text Solution
|