Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
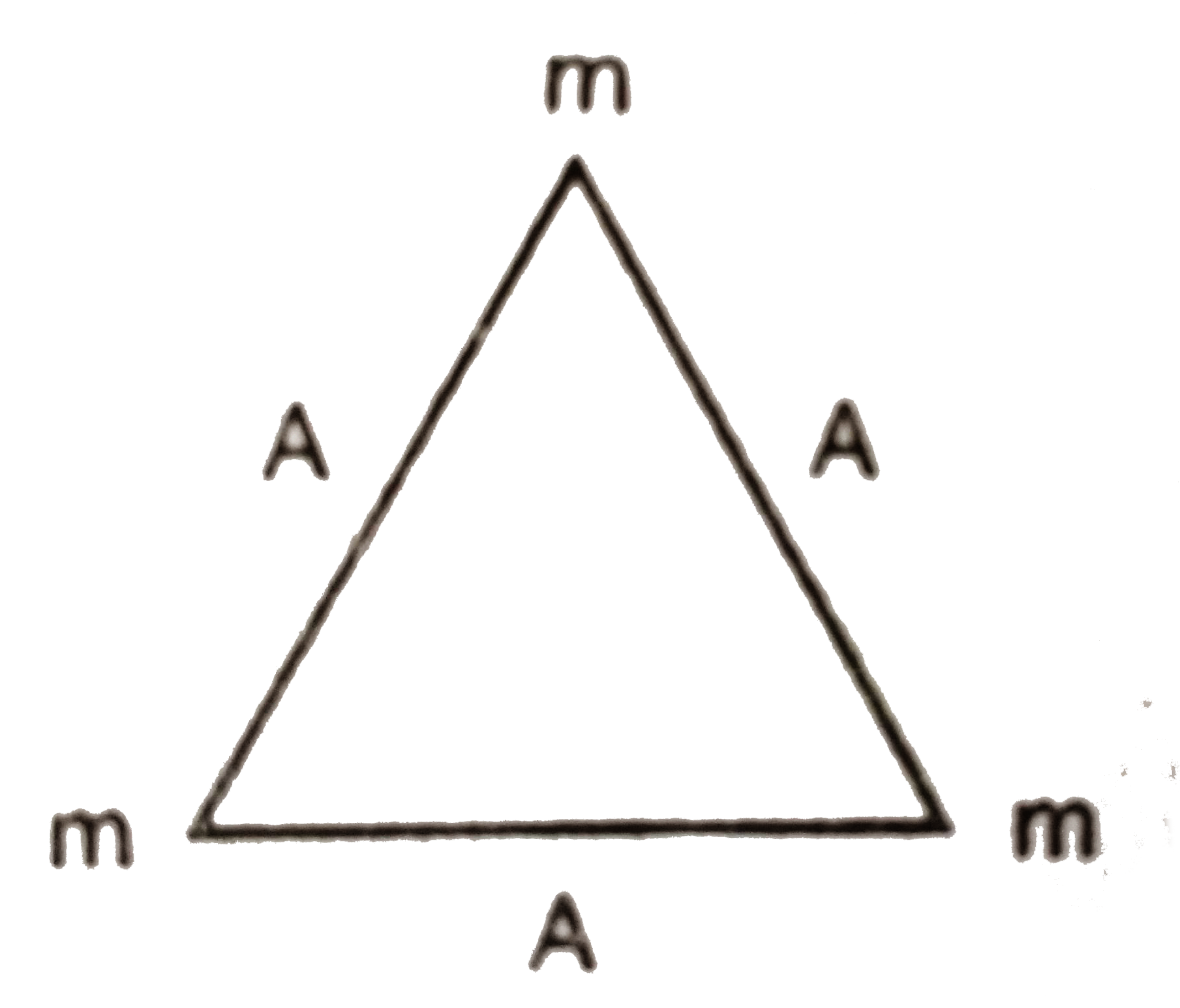
- Three particle of mas m each are placed at the three corners of an equ...
Text Solution
|
- Three particle of mas m each are placed at the three corners of an equ...
Text Solution
|
- (a) Three particles of mass m each are placed at the three corners of ...
Text Solution
|
- तीन कण, प्रत्येक का द्रव्यमान m, भुजा a वाले समबाहु त्रिभुज के तीन कोन...
Text Solution
|
- a भुजा वाले समबाहु त्रिभुज के तीनों कोनो पर एक- एक कण रखे गए है ...
Text Solution
|
- Three particles each of mass m are placed at the three corners of an e...
Text Solution
|
- Three particles each of mass m are placed at the three corners of an e...
Text Solution
|
- Three particles each of mass m are palced at the corners of an equilat...
Text Solution
|
- Three particle of mas m each are placed at the three corners of an equ...
Text Solution
|