Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
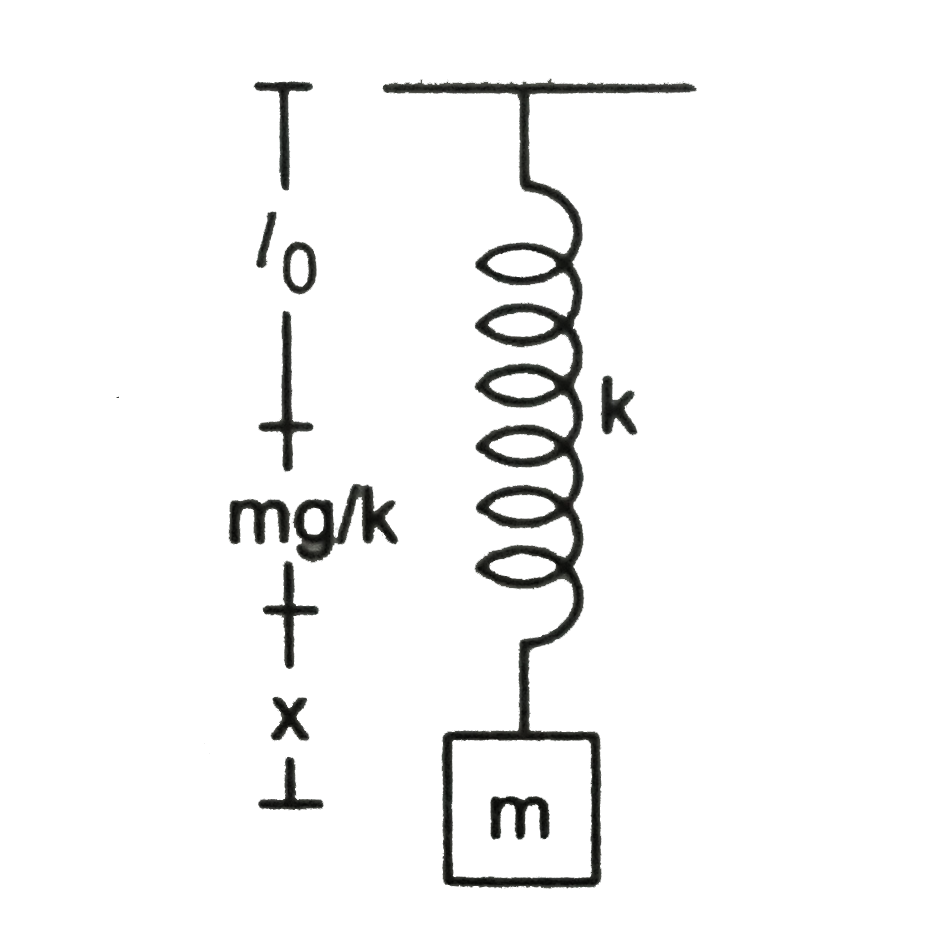
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- Figure shows a system consisting of a massless pulley, a spring of for...
Text Solution
|
- A block of mass m is connected with two ideal pullies and a massless s...
Text Solution
|
- The period of oscillation of a mass M suspended from a spring of sprin...
Text Solution
|
- A body of mass 'm' hangs from three springs, each of spring constant '...
Text Solution
|
- Find the time period of oscillation of block of mass m. Spring, and pu...
Text Solution
|
- A block of mass m hangs from three springs having same spring constant...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|