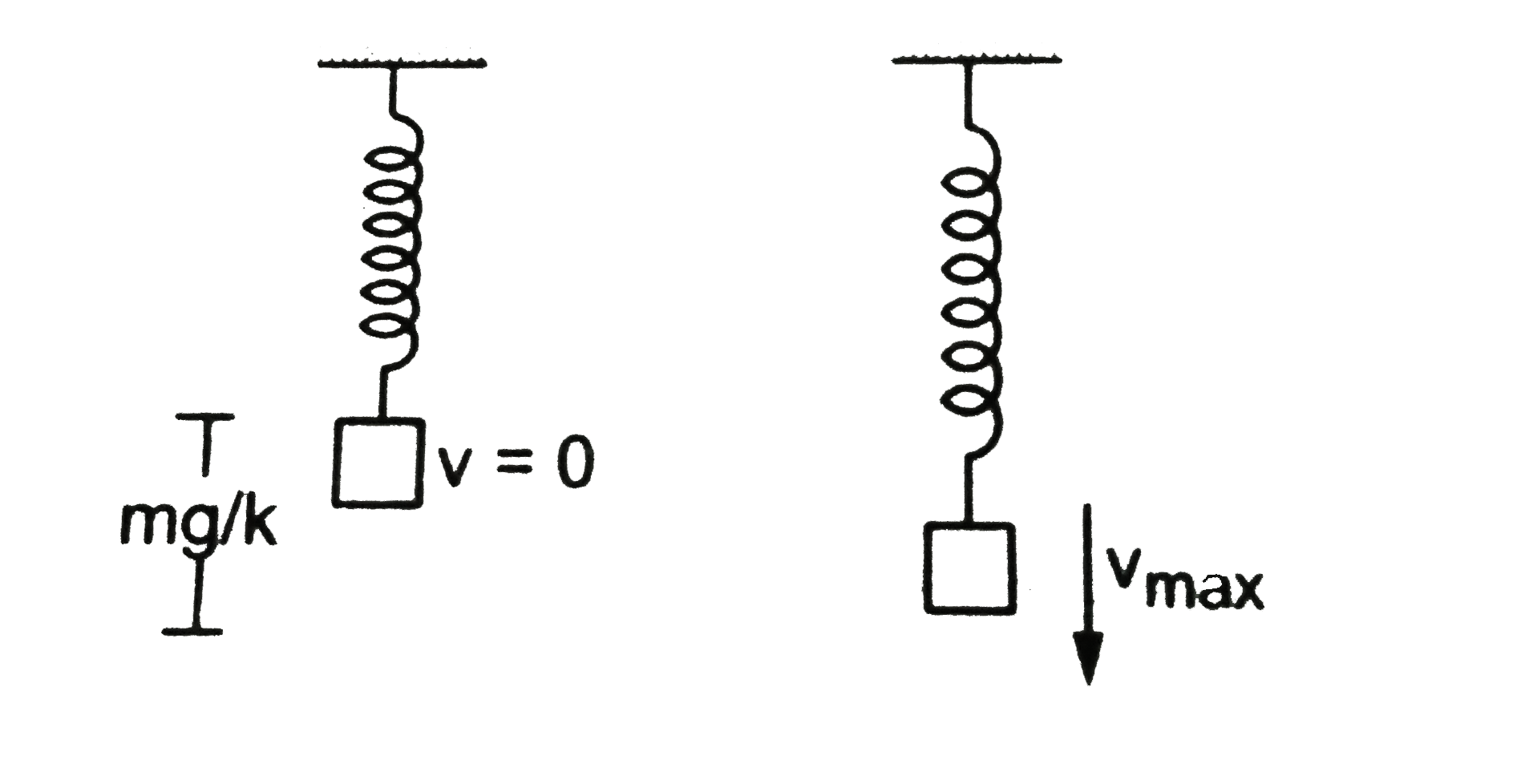
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle suspended from a vetical spring oscillastes 10 times per s...
Text Solution
|
- A particle suspended from a vetical spring oscillastes 10 times per s...
Text Solution
|
- Frequency of a particle executing SHM is 10 Hz. The particle is suspen...
Text Solution
|
- Frequency of a particle executing SHM is 10Hz . The particle is suspen...
Text Solution
|
- Frequency of a particle executing SHM is 10 Hz. The particle is suspen...
Text Solution
|
- एक वस्तु एक ऊर्ध्वाधर स्प्रिंग से लटकी हुई है और प्रतिसेकण्ड 10 दोलनम ...
Text Solution
|
- A particle suspended from a vertical spring oscillates 10 times per se...
Text Solution
|
- A particle suspended from a vertical spring oscillates 8 times per sec...
Text Solution
|
- A particle suspended from a vertical spring oscillates 10 times per se...
Text Solution
|