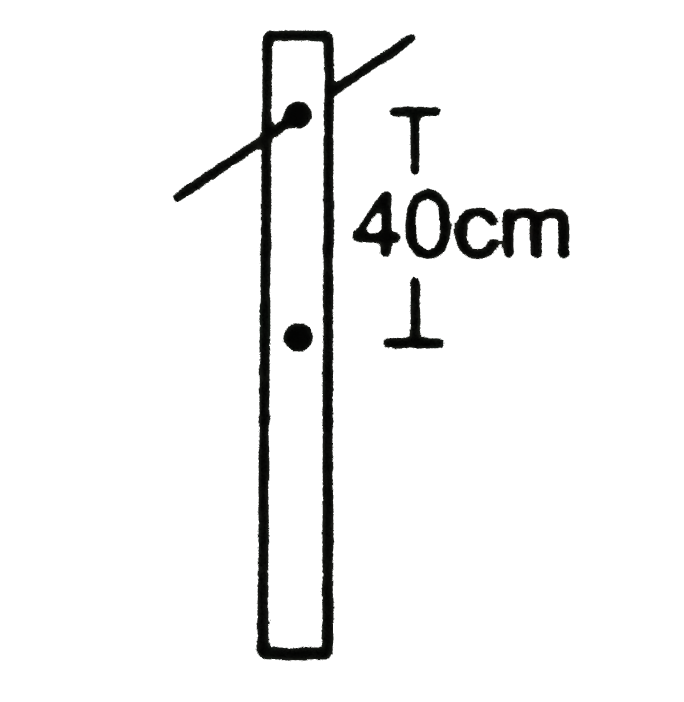
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform meter stickis suspended through a small pin hole at the 10 c...
Text Solution
|
- A uniform rod of length 1.00 m is suspended through an end and is set ...
Text Solution
|
- A uniform meter stickis suspended through a small pin hole at the 10 c...
Text Solution
|
- A uniform rod of mass m and length l is suspended through a light wire...
Text Solution
|
- A uniform disc of radius r is to be suspended through a small hole mad...
Text Solution
|
- Find the time period of small oscillations of the following systems. ...
Text Solution
|
- A uniform ring of radius 'R' is suspended from a horizontal nail 'A' a...
Text Solution
|
- A uniform rod of length 2.0 m is suspended through an end and is set i...
Text Solution
|
- एक मीटर लम्बी एक समरूप छड़ में किनारे से 10 cm दूर एक छोटा छेद किया गया...
Text Solution
|