Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
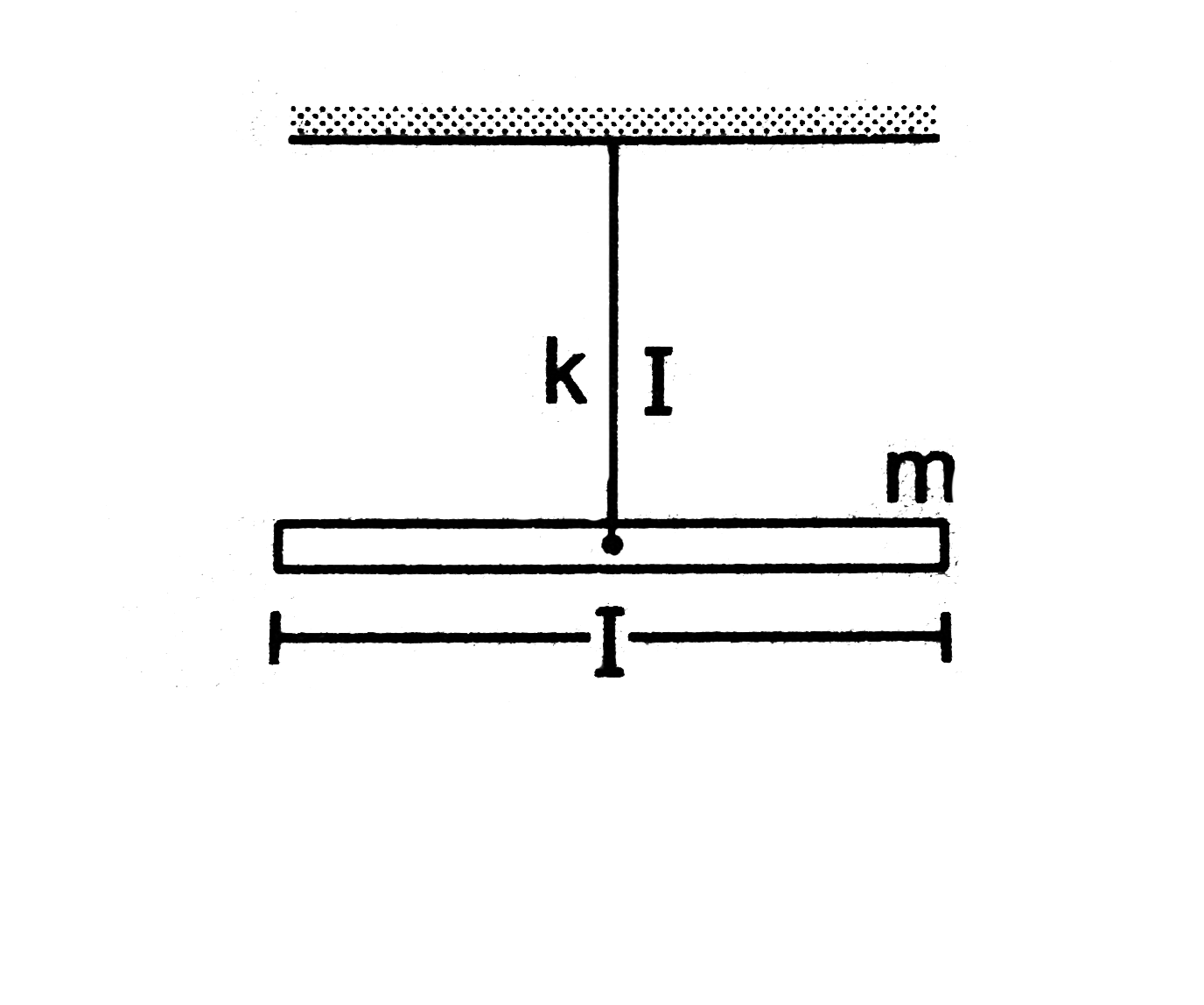
- A uniform rod of mass m and length l is suspended through a light wire...
Text Solution
|
- A uniform rod of mass m and length l is suspended through a light wire...
Text Solution
|
- Two small balls, each of mass m are connected by a light rigid rod of ...
Text Solution
|
- Two identacal rods each of length l and mass m weided toeather at righ...
Text Solution
|
- Find the frequency of small oscillations of thin uniform vertical rod ...
Text Solution
|
- A uniform rod AB of mass m and length L rotates about a fixed vertical...
Text Solution
|
- A square plate of mass M and side length L is hinged at one of its ver...
Text Solution
|
- A rod of mass m and length l is rotating about a fixed point in the ce...
Text Solution
|
- Consider the situation shown in the figure. Uniform rod of length L ca...
Text Solution
|