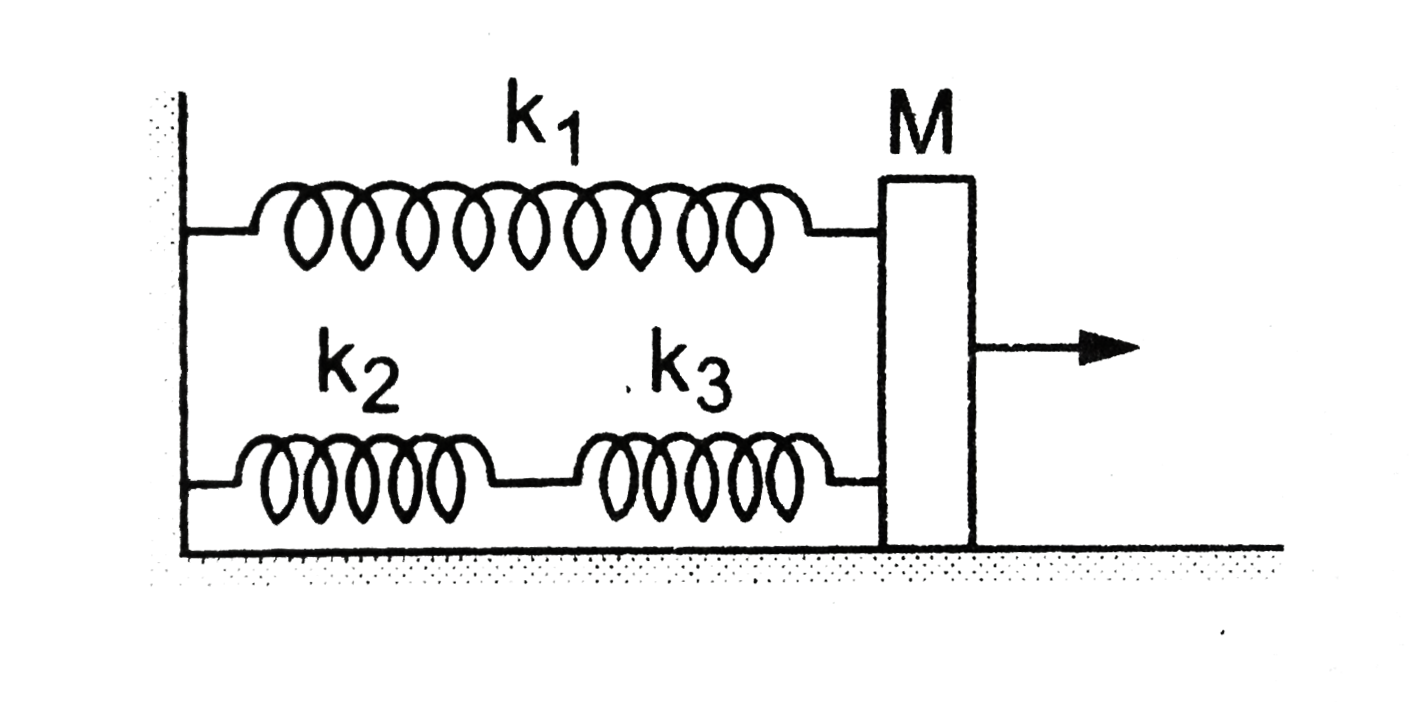Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The springs shown in the figure are all unstretched in the beginning w...
Text Solution
|
- The springs shown in the figure are all unstretched in the beginning w...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- The spring shown in figure is unstretched when a man starts pulling on...
Text Solution
|
- The springs shown in the figure are all upstretched in the beginning w...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A spring mass systeam is shown in figure, spring is initially unstretc...
Text Solution
|
- Initially block shown is at rest and the spring is unstretched, when a...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|