Text Solution
Verified by Experts
Topper's Solved these Questions
MAGNETIC FIELD DUE TO CURRENT
HC VERMA|Exercise Short Answer|12 VideosMAGNETIC FIELD DUE TO CURRENT
HC VERMA|Exercise Objective 1|12 VideosMAGNETIC FIELD DUE TO CURRENT
HC VERMA|Exercise Exercises|61 VideosMAGNETIC FIELD
HC VERMA|Exercise Exercises|61 VideosMAGNETIC PROPERTIES OF MATTER
HC VERMA|Exercise Exercises|9 Videos
Similar Questions
Explore conceptually related problems
HC VERMA-MAGNETIC FIELD DUE TO CURRENT-Worked Out Examples
- Two long wires a and b, carrying equal currents of 10*0A, are placed p...
Text Solution
|
- Two parallel wires P and Q placed at a separation d= 6 cm carry el...
Text Solution
|
- Two long, straight wires a and b are 2*0 m apart, perpendicular to t...
Text Solution
|
- A current of 2*00 A exists in a square loop of edge 10*0 cm. Find the ...
Text Solution
|
- Figure shows a square loop made from a uniform wire. Find the magnet...
Text Solution
|
- Two long wires, carrying currents i1 and i2, are placed perpendicular...
Text Solution
|
- Figure shows a part of an electric circuit. ABCD is a rectangular loop...
Text Solution
|
- Figure shows a current loop having two circular arcs joined by two rad...
Text Solution
|
- Find the magnetic field at the point P in figure. The curved portion i...
Text Solution
|
- The magnetic field B due to a current- carrying circular loop of radiu...
Text Solution
|
- Consider a coaxial cable which consists of an inner wire of radius a s...
Text Solution
|
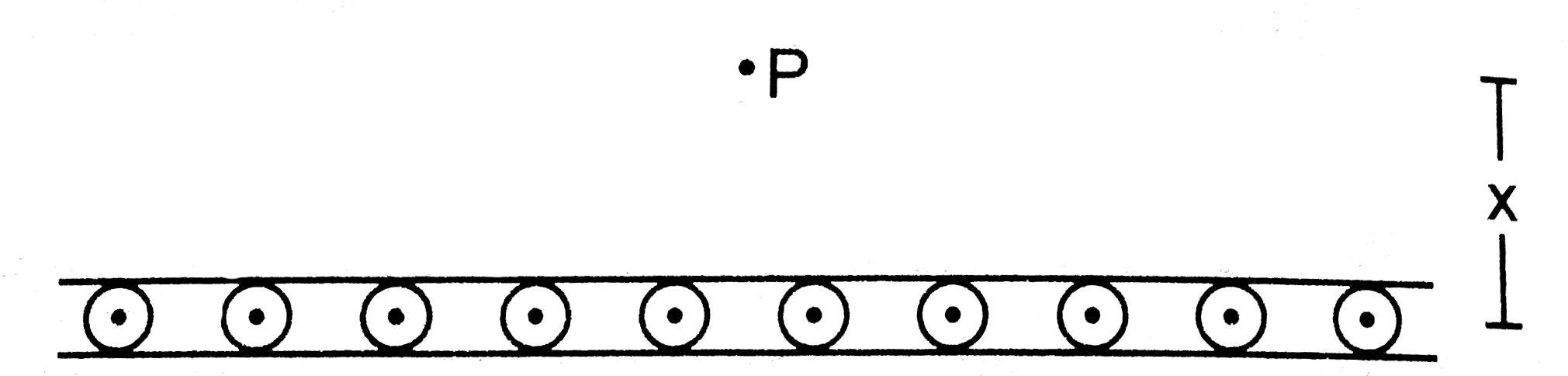
- Figure shows a cross section of a large metal. Sheet carrying an elect...
Text Solution
|
- Consider the situation described in the previous example. A particle o...
Text Solution
|
- Three identical long solenoids P,Q and R are connected to each other a...
Text Solution
|
- A long , straight wire carries a current i. A particle having a positi...
Text Solution
|